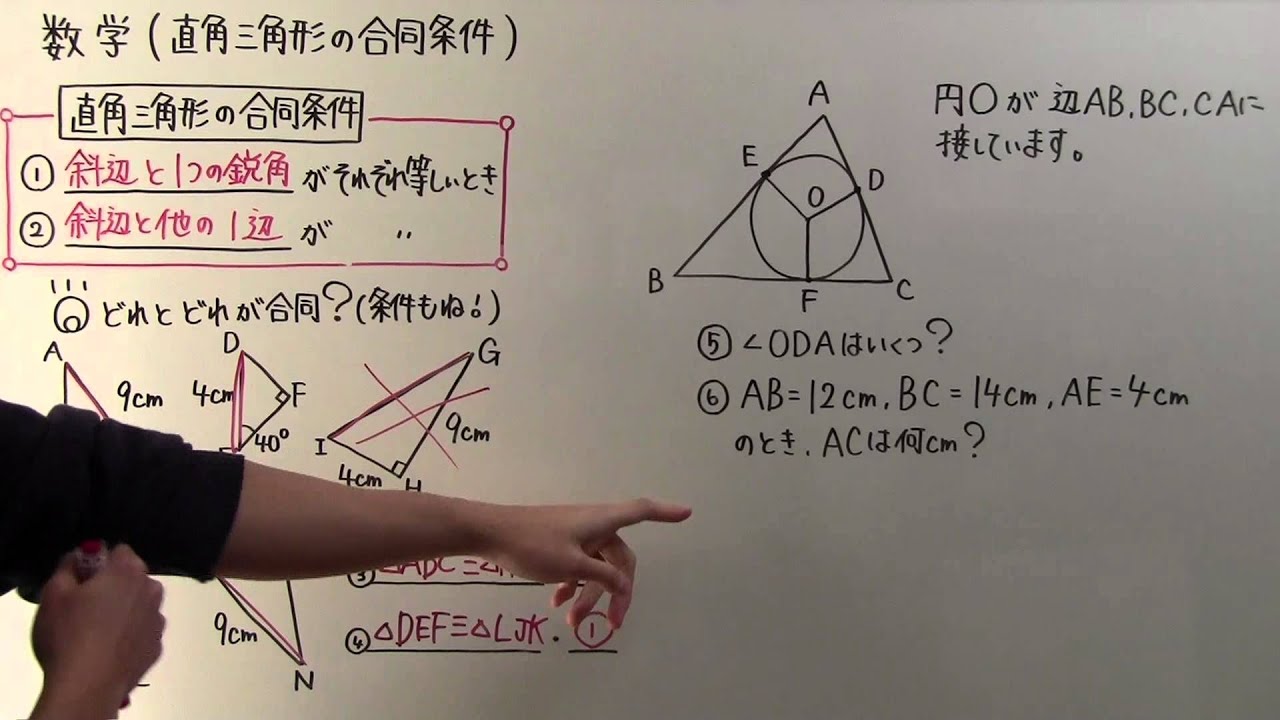
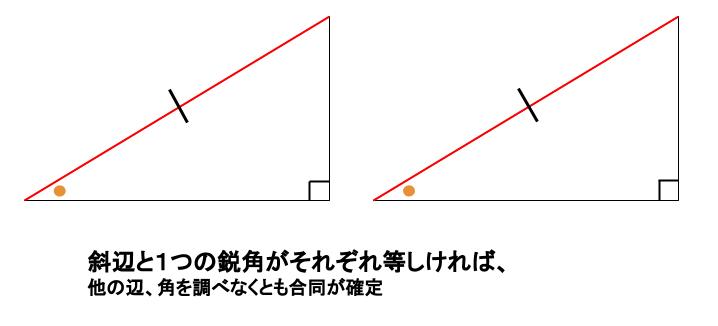
直角三角形の合同条件のポイントは! 直角三角形とは1つの角が直角である三角形のこと 直角の向かいにある辺のことを斜辺という 直角三角形の直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明) 直角三角形は、角の1つが直角であるために、合同条件は見た目が緩くなります。 合同条件は次の通りです。 直角三角形の合同条件 斜辺と他の1組の辺がそれぞれ相等しい 斜辺と直角でないの1組の角がそれぞれ相等しい それぞれ見ていきましょう。 斜辺と他の1辺 斜辺がそれぞれ相等しい
数学 中2 71 直角三角形の合同条件 Youtube
三角形 合同条件 直角三角形
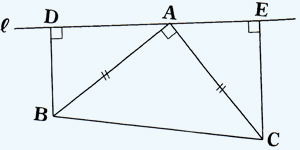
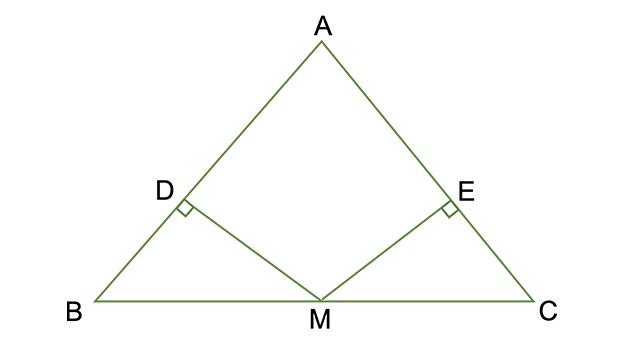
三角形 合同条件 直角三角形- 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件 3組の辺の比がすべて等しい 2組の辺の比とその間の角がそれぞれ等しい 直角三角形の合同条件2つ まず、一般的な三角形における合同条件3つについて三角形の合同の証明 三角形の合同の証明③ 下の図で,ac°db,cm=dm である。 このとき,¼acm×¼bdm であること を右のように証明した。 下線部をうめて, 証明を完成させなさい。



証明直角三角形に三角形の合同条件 先程 直角三角形の証明を解いていて Yahoo 知恵袋
直角三角形とは?定義や定理、辺の長さの比、合同条件 🙌 直角三角形が2つくっついてる問題 つぎは、 直角三角形が2つくっついてる問題な。 問題1 この三角形は、正方形をひとつの対角線で分割してでき 直角三角形の合同条件 2 2 つの三角形がともに直角三角形であるとわかっている場合は,それらが合同かどうかを確かめることはより簡単になります.つまり,先にみたような一般の三角形に対する合同条件よりも少ない情報で,合同かどうかを確かめる 直角三角形の合同条件 2つの直角三角形において、次の2つの条件のうちどちらかが成り立つとき、その直角三角形は合同であるといえます。 斜辺と1つの鋭角がそれぞれ等しい 斜辺と他の1辺がそれぞれ等しい 直角三角形の証明問題
直角三角形の辺の長さ・合同条件・面積について|アタリマエ! 直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき \(a×ab×b=c×c\) が成り立つことが分直角三角形の合同条件では、この 「斜辺」 が主役。 「斜辺」 と 他の1辺 か、 「斜辺」 と 1つの鋭角 がそれぞれ等しければ合同になるんだ。・三角形の合同条件を理解し,三角形が合同かどうかを三角形の合同条件をみつけ,説明する ことができる。 (2)観点別評価規準 ・様々な事象を平行線の性質,三角形の角についての性質,三角形の合同条件などで捉えようと している。ア①
直角三角形の合同条件 直角三角形は,1つの角度が 9 0 ∘ 90^{\circ} 9 0 ∘ であるため,特有の合同条件を持ちます。 そんなの簡単だよ。 ABCと GHIで、合同条件は「直角三角形の斜辺と他の1辺がそれぞれ等しい」です! 確かに ABCと GHIは合同ですね。 でも,当てはまる合同条件は本当にそうかな? この2つの直角三角形の斜辺てどこだろう? えーと、斜辺は辺ABとGHで 三角形の合同条件 私は現在高一なんですが、三角形の合同条件に少し疑問があります。三角形の合同条件といえば、 ・3辺が全て等しい ・2辺とその挟む角が等しい ・1辺とその両端の角が等しい ですけど、この2つ目と3つめに疑問があるんです。




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題
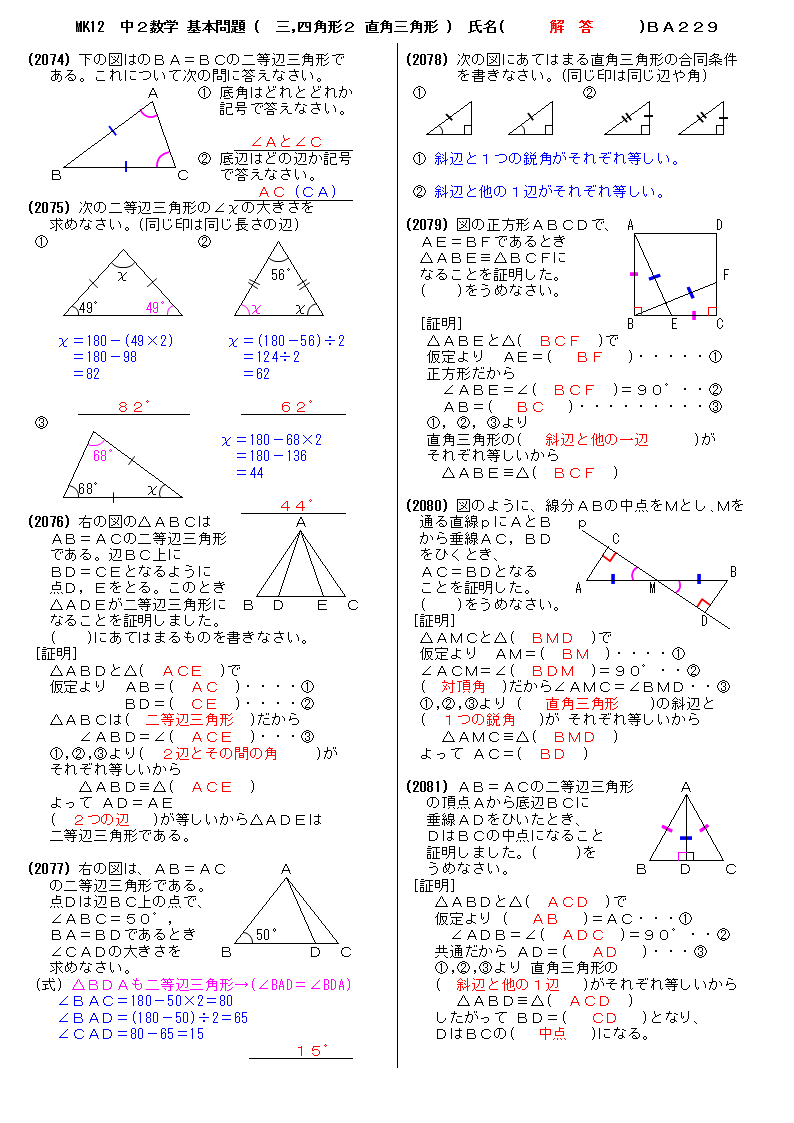



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形
八年级上册数学学案编写人陆香姣审核人其他组员☆数学是对真善美的追求☆班级_____姓名_____ page page 18 第一章直角三角形第6课时13直角三角形全等的判定学习目标1探索两个直角三角形全等的条件2掌握两个直角三角形全等的判定定理hl自学导航阅读教材完成探究作一个使90°把所画的剪下来将你和このとき、三角形の合同条件を参考にすることを確認する。 練り合う 数学的活動 〔観察、操作などの具体的な活動〕 ・斜辺と1つの鋭角がそれぞれ等しい場合と、斜辺と他の1辺がそれぞれ等しい 場合に分けて考える。 ・実際に、画用紙で作った直角次時につなげるために次のような発問をし,三角形の合同条件の価値付けをします。 三角形の合同条件として3つにまとめましたが,どんな良さがありますか。 辺と角,6組を全部調べなくても,3組で合同であるかどうか判断できます。 S




授業料無料 中2数学 直角三角形の合同条件2 連問1 Youtube



直角三角形の合同証明 難 の解説 春日井市高蔵寺の学習塾 西村セミナールーム
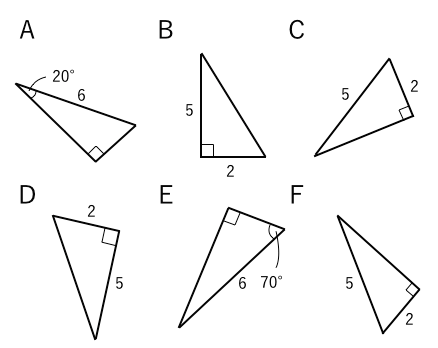
三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これから証明問題へ進んでいく上で 必要となってくるものなので ぜーーーーったいに覚えておきましょう! また、合同な 問2 下の図の三角形を、合同な三角形の組に分けなさい。また、そのとき使った合同条件をいいなさい。 3㎝ 3㎝ 3㎝ 3㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 70° ° ア イ ウ エ オ カ※ 特に,直角三角形では相似条件の③により 直角以外のもう一つの角が等しければ相似ということになります。 直角三角形の合同条件には、以下の \(2\) つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい \(1\) つの角が \(90^\circ\) であることから、斜辺の長さおよび \(1\) つの鋭角が等しいことが示せれば、 残りの \(1\) 角も自ずと定まります 。




ぜいたく直角三角形相似条件 壁紙配布




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
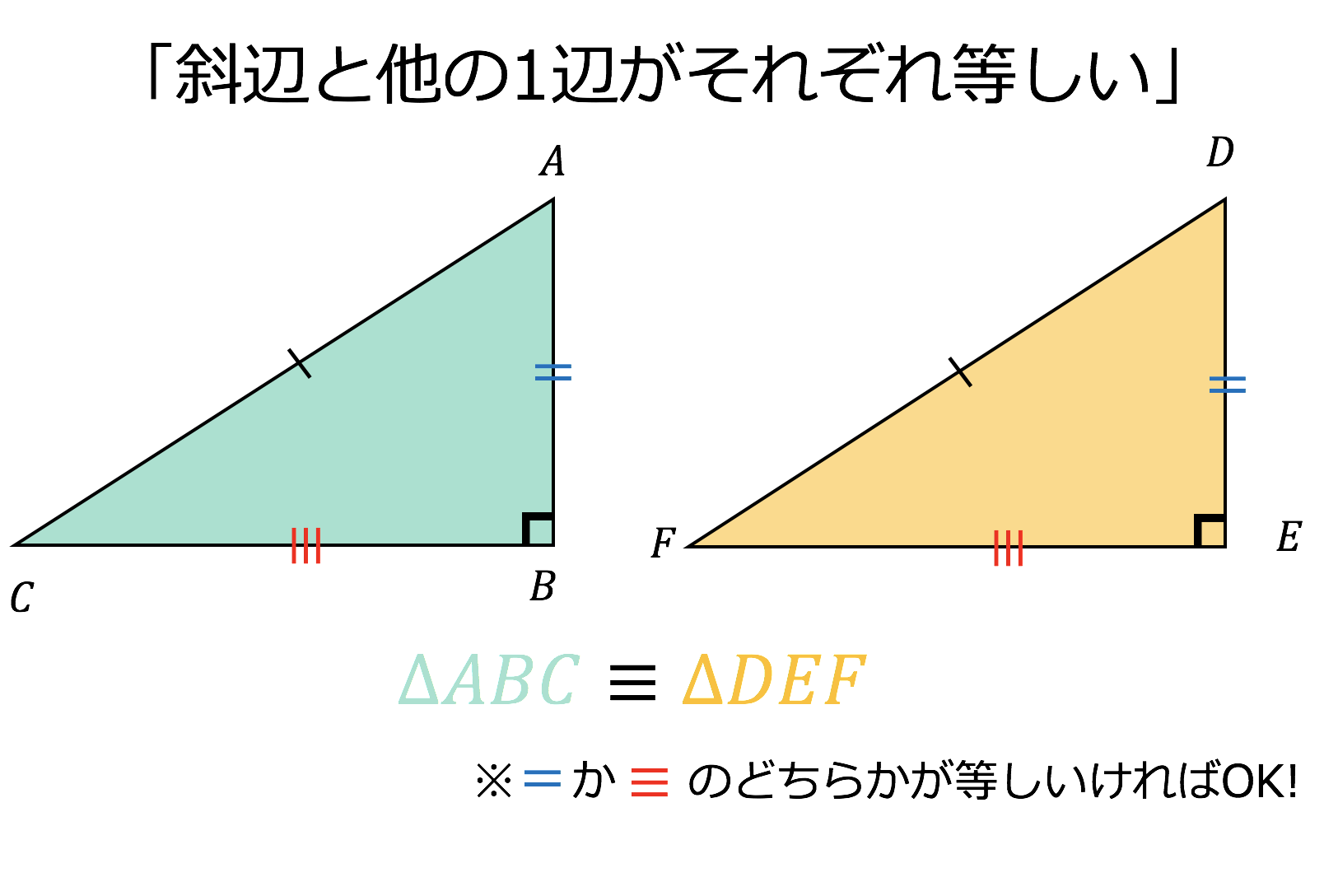
形について の問題が中心であったこと。4つめは,高等小学校の第2期~第3期改訂では,三角形 合同条件を論証するが,三角形の合同条件は図形を作図するための保証の役割として位置付けていた ことである。 検索語高等小学校,合同条件,論証,作図 1研 究の目的 直角三角形の合同条件で、三辺相等のように漢字で省略されたものはありますよね? Yahoo!知恵袋 直角三角形の合同条件で、三辺相等のように漢字で省略されたものはありますよね? 学校で斜辺1鋭角相等と言ったら違うと言われました 直角三角形の直角三角形の合同条件とは 直角三角形は、以下のことが分かれば合同だと言えます。 今までの三角形の合同条件が このように、3つの情報を組み合わせて合同を言うことができましたが 直角三角形の場合には このように2つの情報だけでOKになります。 ちょっと便利ですね (^^) ただし、直角三角形の斜辺が等しいことが前提となっているので注意ですね。



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
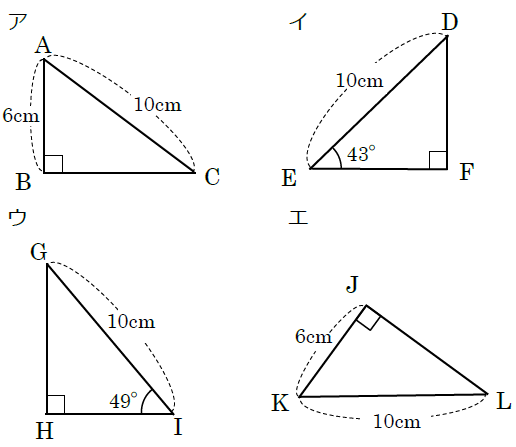
2542 直角三角形の合同条件 問題 1 2つの三角形の合同条件は何でしょうか? 正解 : 直角三角形の斜辺と他の1辺がそれぞれ等しい。 (RHS) 問題 2 2つの三角形の合同条件は何でしょうか? 正解 :直角三角形の斜辺と1つの鋭角がそれぞれ等しい。 (RHA)直角三角形 合同条件 よって、合同条件「1組の辺とその両端の角がそれぞれ等しい」を満たします。 HI=LK=8cm、∠H=∠L=80°、∠I=∠K=30° なので 直角三角形の合同条件とは 直角三角形の合同条件は「普通の三角形の合同条件」に2つの条件が加わります。 全部で5つの条件があり、これらのうちどれか1つでもあてはまれば、「合同である」と言えます 直角三角形 辺角辺これが基本の三角形の合同条件 角角辺相似かつ相似比が11なら合同だ 辺辺辺三角形のみに成り立つ特殊な合同条件 (4辺が等しい四角形は合同とは限らない) 辺辺90°直角三角形の合同条件




直角三角形の合同条件 小学生 中学生の勉強



直角三角形の合同 証明問題 苦手な数学を簡単に
三角形 合同条件 2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。ある 2 つの三角形について、




直角三角形の合同条件について考えてみた ブログ サイバー少年



フロー 2 5 4 4 直角三角形の合同条件を利用した証明




3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




探索直角三角形全等的条件演示文稿下载 Ppt模板 爱问共享资料




直角三角形の合同の証明の問題です わからないので教えてください お願いします Clear




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材




初二数学 直角三角形 学习目标和经典例题 数学老师手写教案 网易订阅




在一直角三角形中 已知高 H 底 L 求钭边上o点在底边上的投影长度 雨露学习互助




直角三角形の合同条件 中学数学 By じょばんに マナペディア
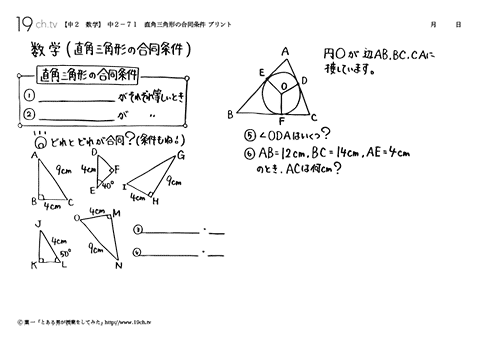



中学2年の数学 動画 直角三角形の合同条件の問題 19ch




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく
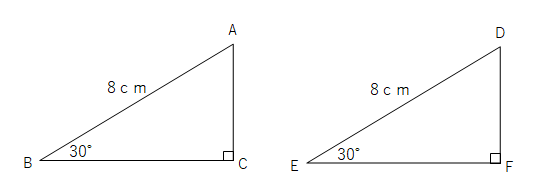



中2数学 直角三角形の合同証明のポイントと練習問題 Examee




直角三角形角度和边长比例 直角三角形边长比例与角度比例有关系吗 三人行教育网 Www 3rxing Org




数学 中2 71 直角三角形の合同条件 Youtube




全等三角形hl判定的基本练习下载 Word模板 爱问共享资料



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋
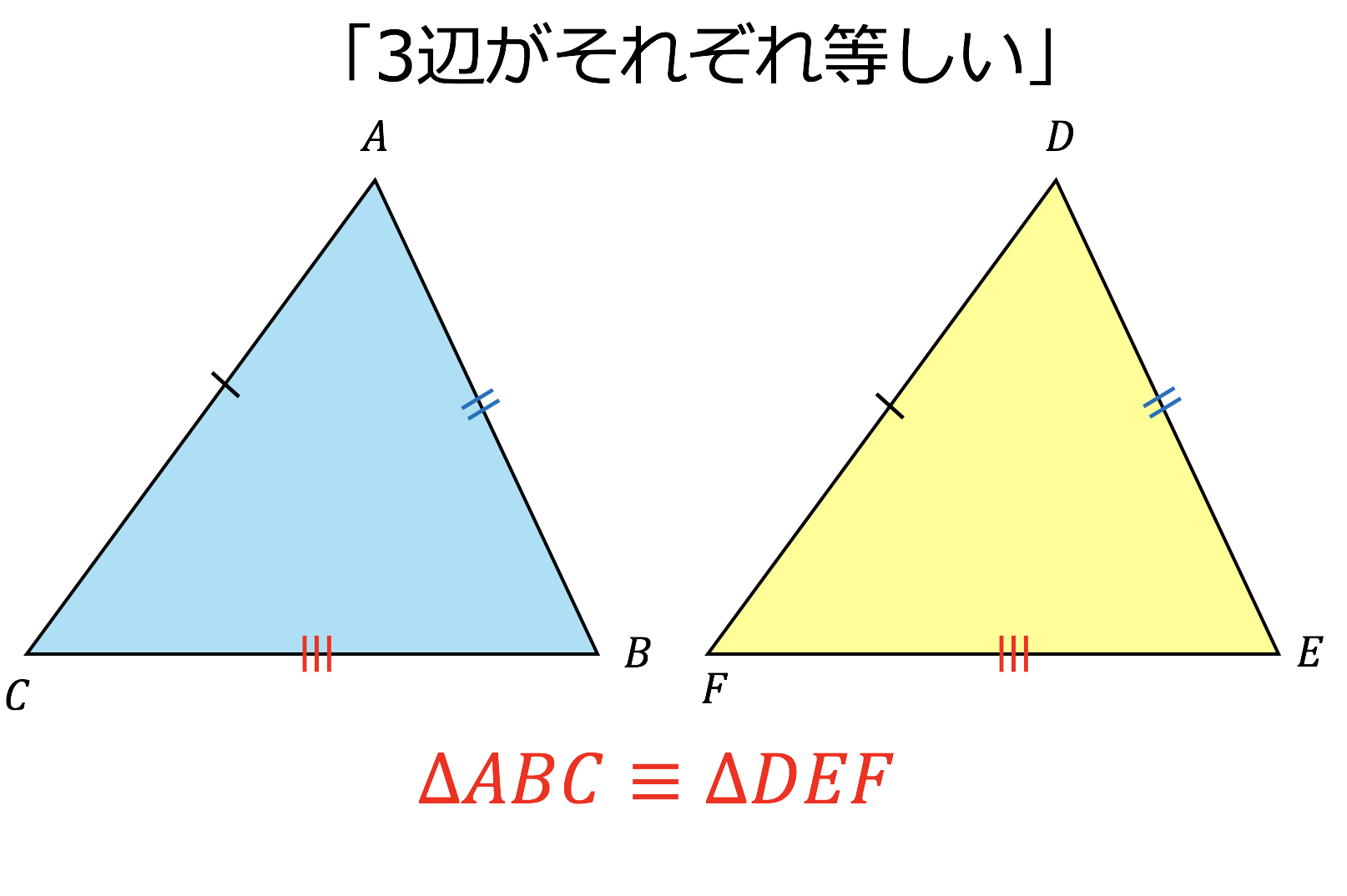



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ
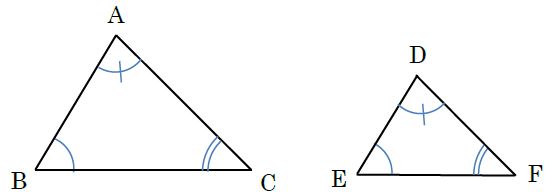



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




直角三角形の合同条件とその証明 数学fun




2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear
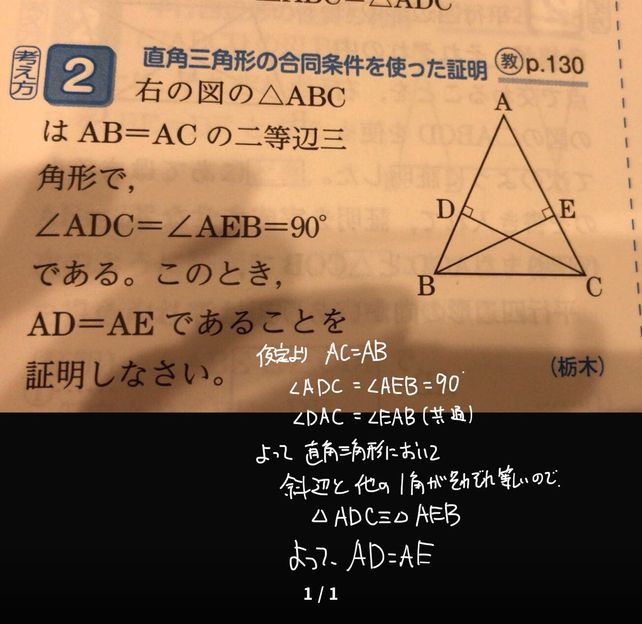



P130 Descubre Como Resolverlo En Qanda
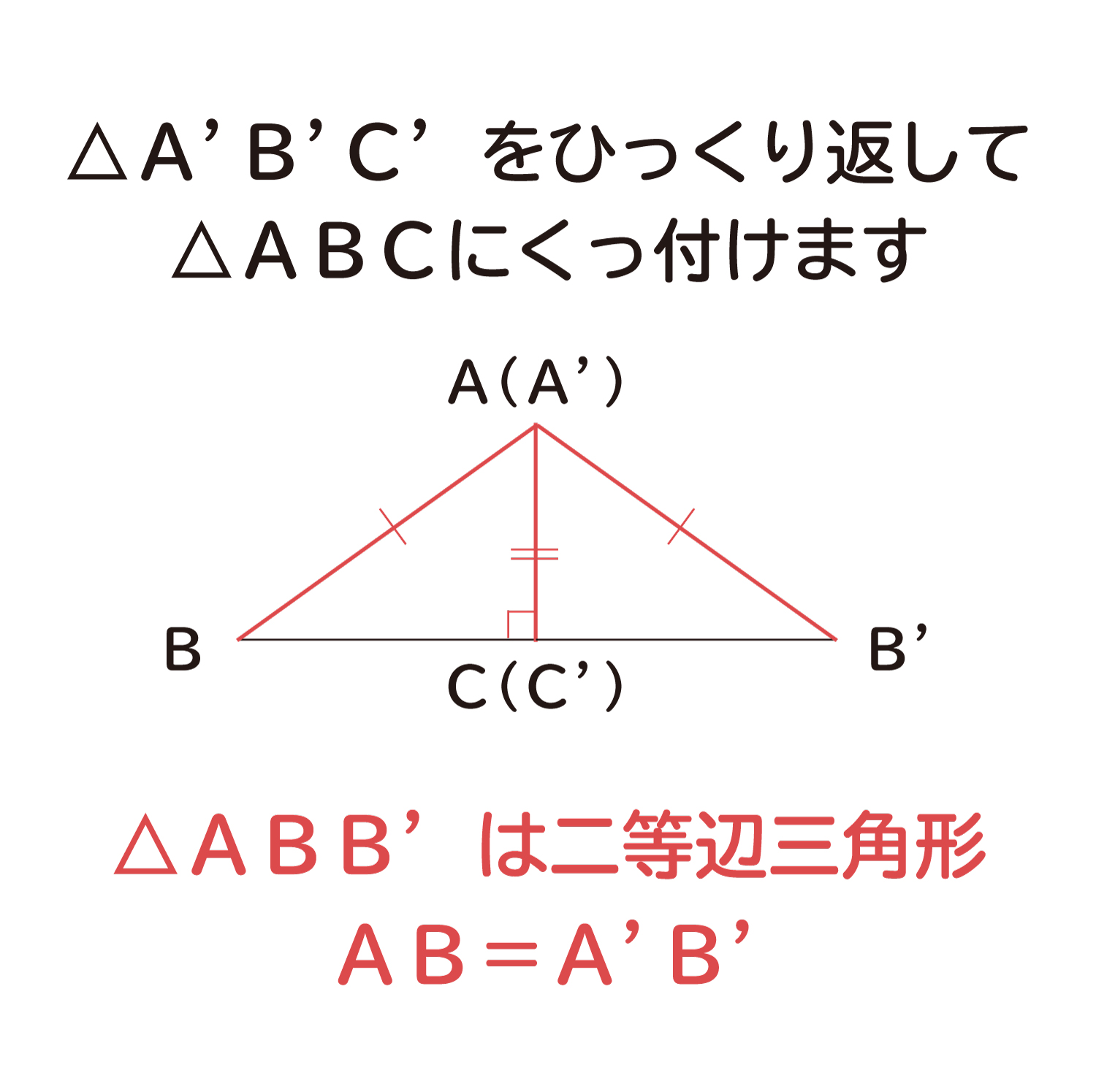



直角三角形の合同条件の説明 おかわりドリル
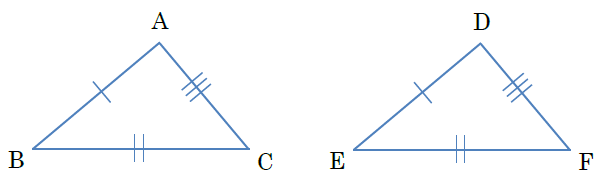



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




三角代换积分法教学体会 参考网




直角三角形英文 三角形 的英文怎么讀 百度知道翻譯此網頁 Dnfiyv




File Diagram Of Proof Of Congruence Condition Of Right Triangle Svg Wikimedia Commons



含30 锐角的直角三角形的性质下载 Word模板 爱问共享资料




三角形の合同条件
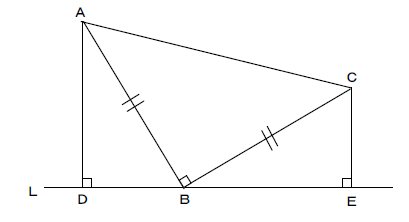



中2数学 直角三角形の合同証明のポイントと練習問題 Atstudier




中2数学 直角三角形の合同条件 例題編 映像授業のtry It トライイット




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
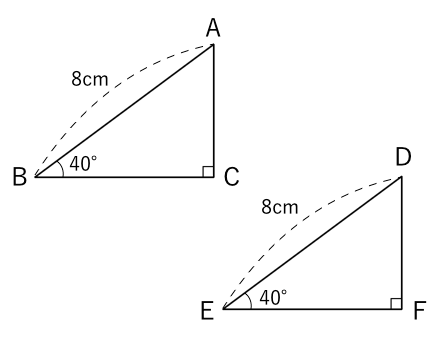



直角三角形の合同 条件 について 苦手な数学を簡単に




本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download
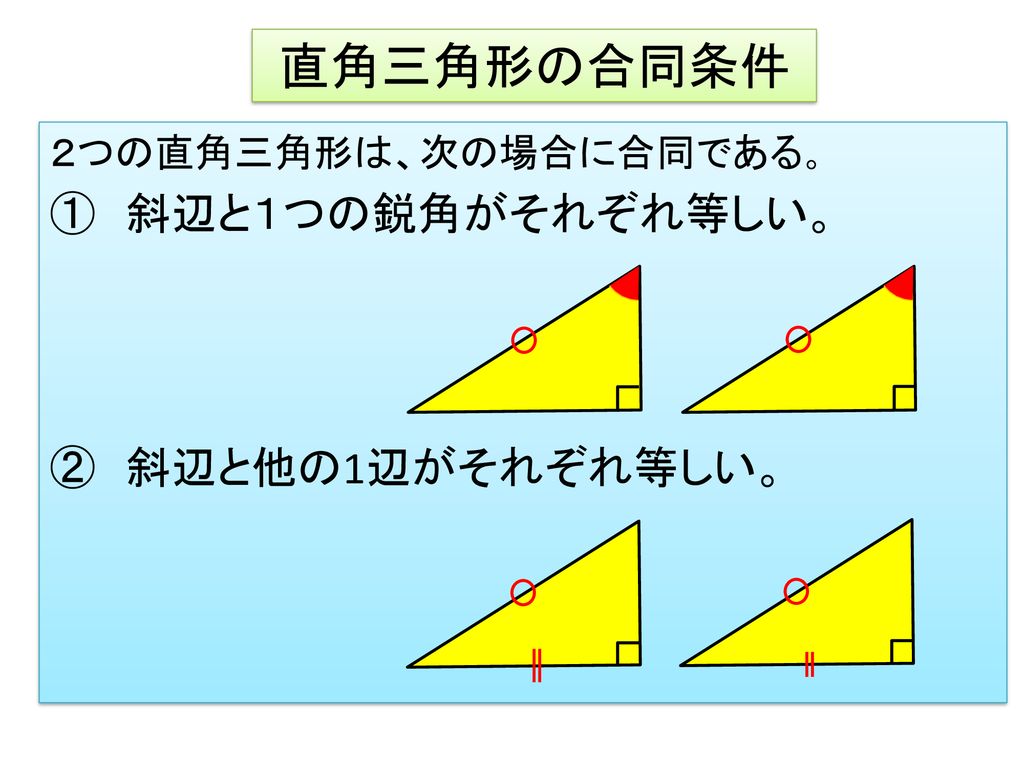



本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download




中2 三角形の性質 直角三角形の合同条件 日本語版 Youtube
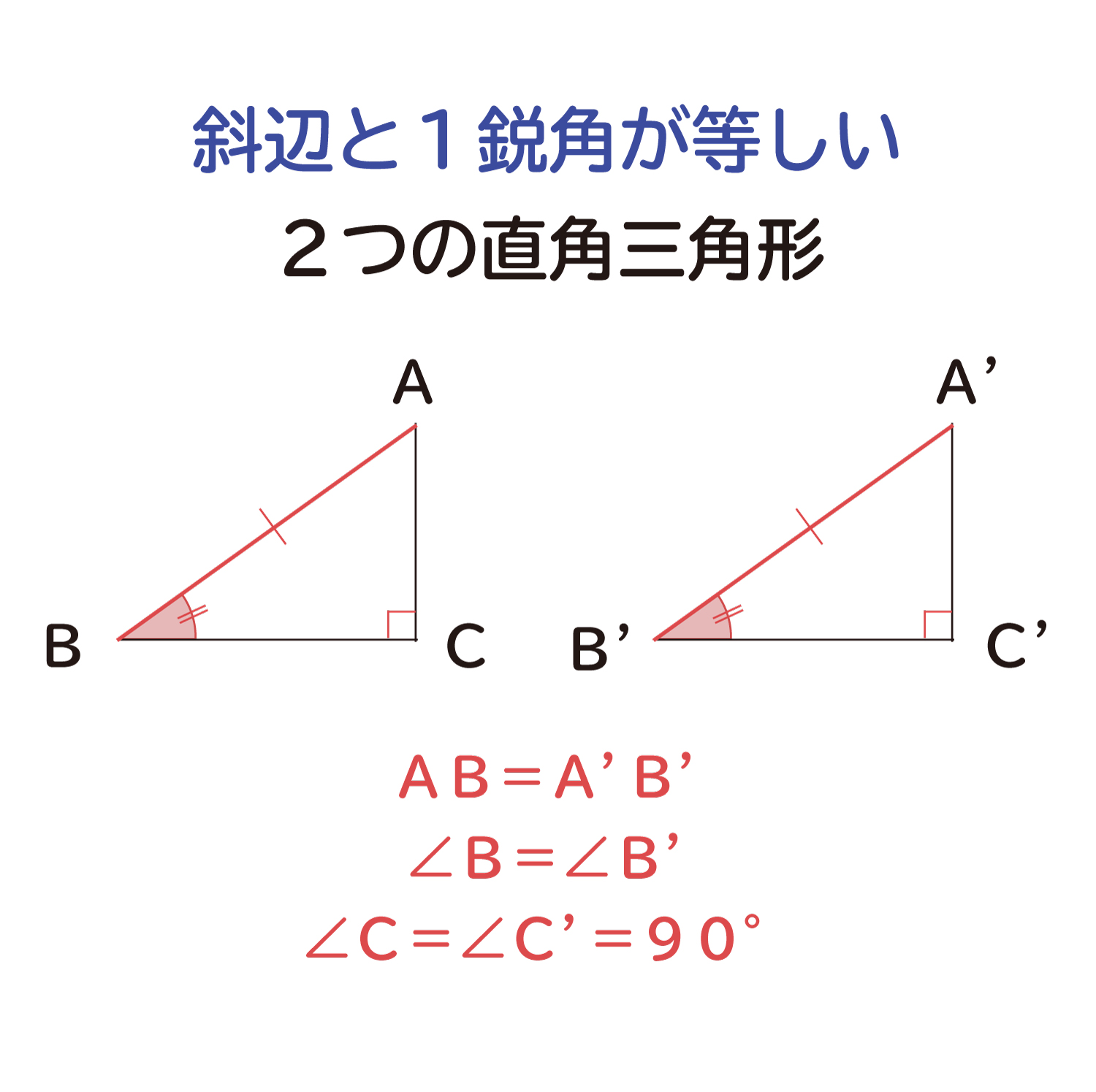



直角三角形の合同条件の説明 おかわりドリル
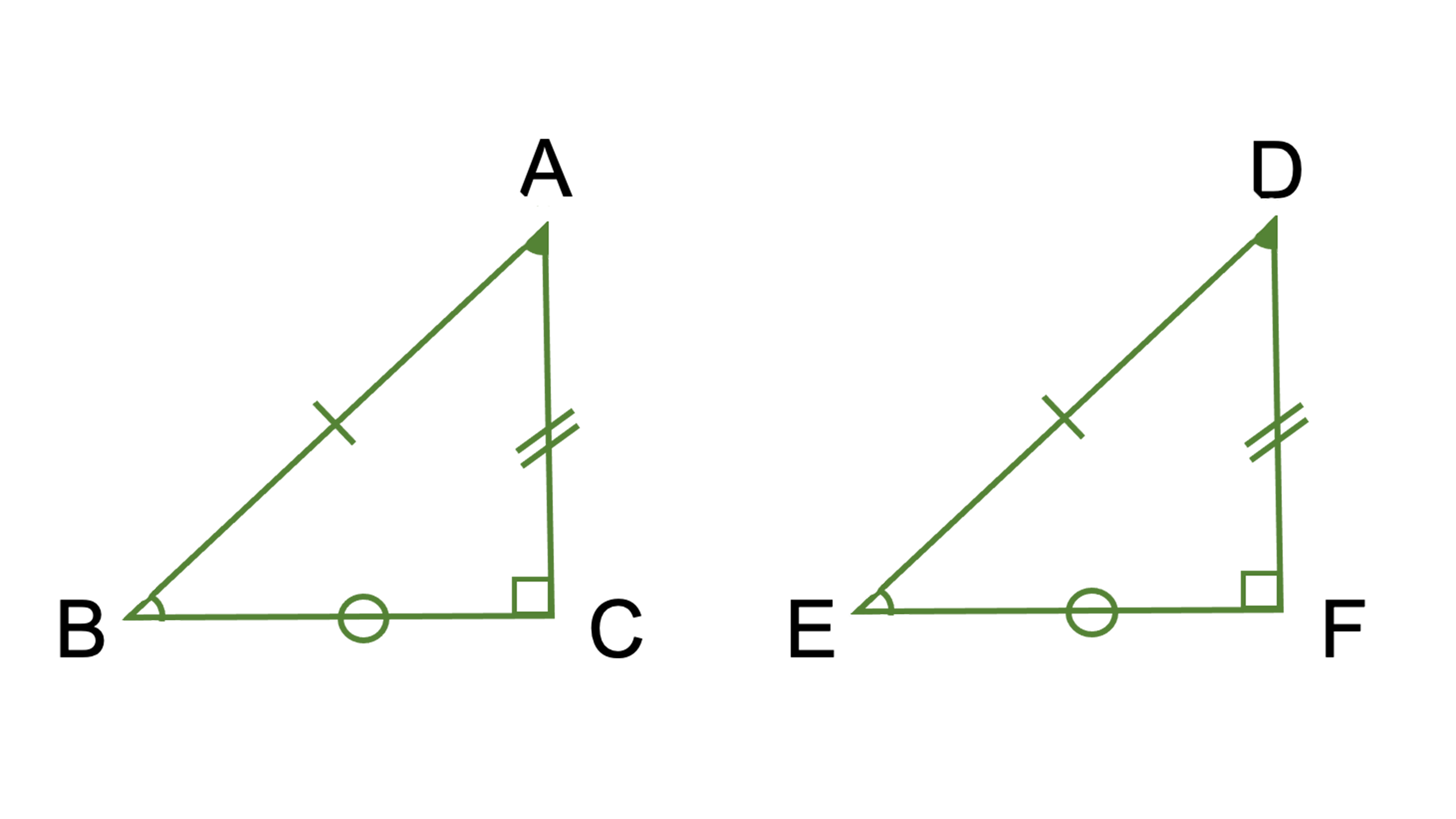



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




Yjj6cr8f9yn5bm
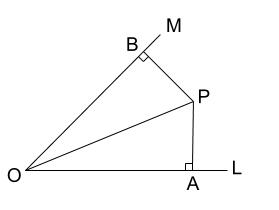



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su
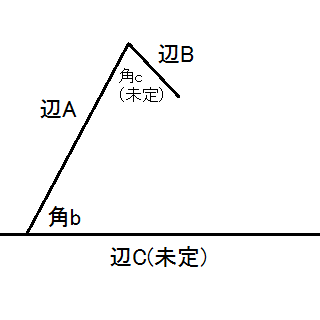



直角三角形の合同条件について考えてみた ブログ サイバー少年




Junior High数学的中2 数学の世界直角三角形の合同条件筆記 Clear




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学




中2数学 直角三角形の合同条件 例題編 映像授業のtry It トライイット



直角三角形の合同条件は 市川中学 10年 算数解法の極意
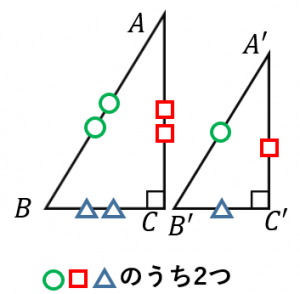



直角三角形の相似条件 具体例で学ぶ数学



1000以上直角三角形相似条件 ニスヌーピー壁紙
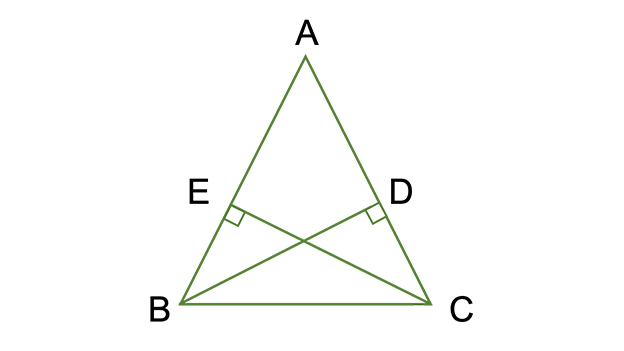



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




初二数学 直角三角形 学习目标和经典例题 数学老师手写教案 网易订阅




初中几何专练 三角形 做完这27道经典题 期末几何部分稳了 数学 直角 多边形 网易订阅




P130 Descubre Como Resolverlo En Qanda




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




直角三角形邊長比三角形的邊長比 Wfklee
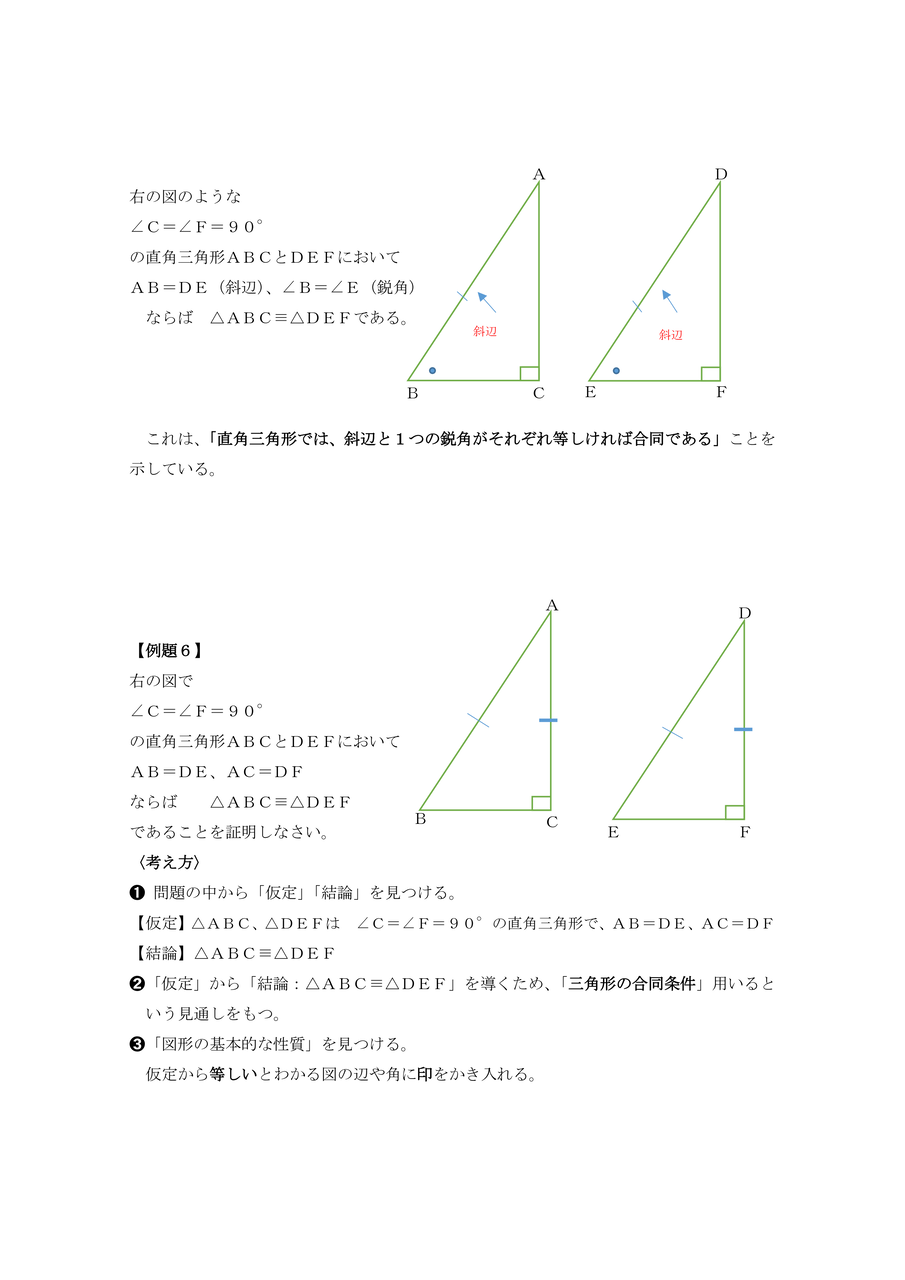



中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材
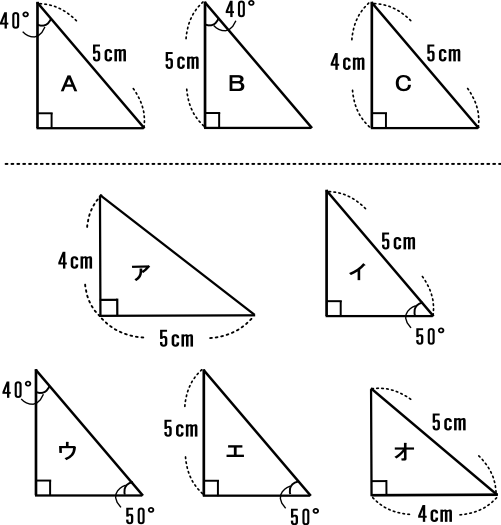



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同
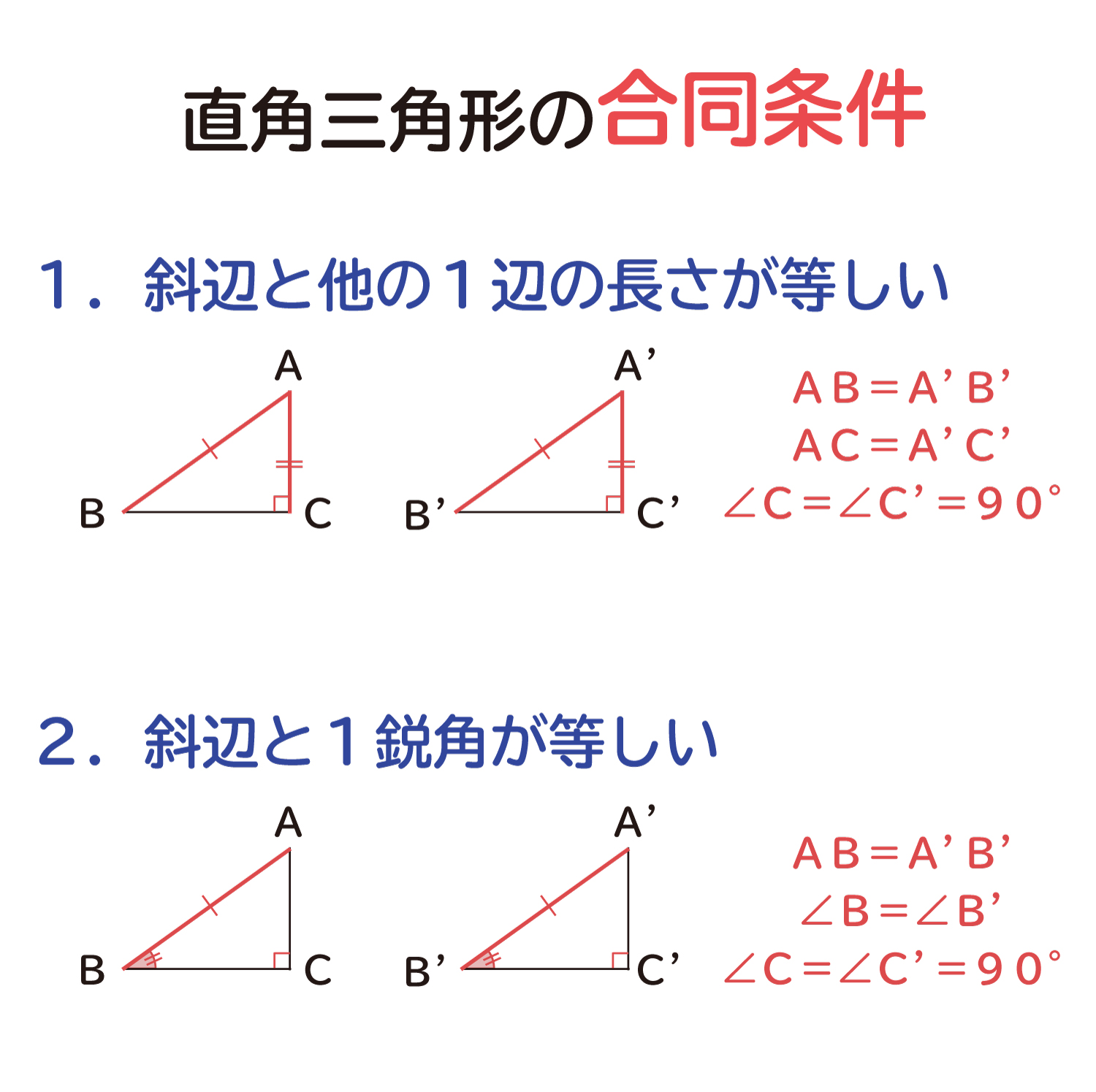



直角三角形の合同条件の説明 おかわりドリル



直角三角形の合同条件 On Vimeo




直角三角形の辺の長さ 合同条件 面積について アタリマエ



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




Ppt 直角三角形の合同 Powerpoint Presentation Free Download Id



直角三角形の合同条件とそれを利用した証明 チーム エン



解直角三角形试题 范文大全网



証明直角三角形に三角形の合同条件 先程 直角三角形の証明を解いていて Yahoo 知恵袋



中2数学 直角三角形の合同の証明のポイントと練習問題 Pikuu




14年中考数学解析版试卷分类汇编专题19 直角三角形与勾股定理下载 Word模板 爱问共享资料



三角形全等的条件 你会几种 5种常用三角形全等辅助线添加方法 有5道例题详解 个税扣除的条件 成人高考的条件 取保侯审的条件 一点通指南网



上数学合同条件 ニスヌーピー壁紙



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
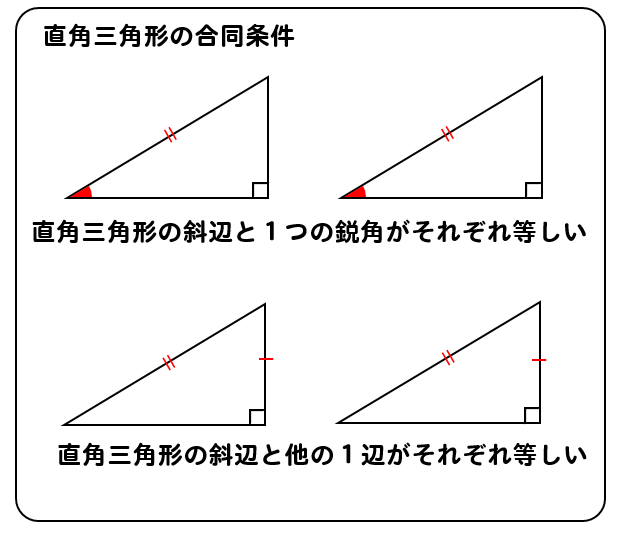



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




E8snuftxl3plnm
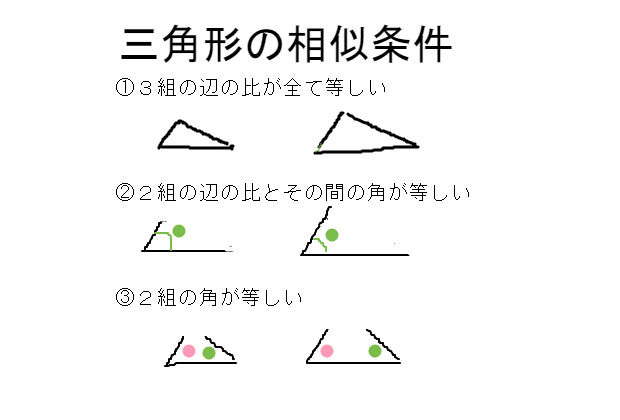



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




A 4 4 Abac Abc Descubre Como Resolverlo En Qanda




直角三角形の合同条件 算数 数学が好きになりmath




直角三角形的边角关系 关于特殊三角形边角关系的总结 Weixin 的博客 Csdn博客




直角三角形の合同条件 小学生 中学生の勉強




直角三角形の合同条件 On Vimeo




直角三角形の合同条件の証明 Youtube




中考数学 二次函数与等腰直角三角形存在性问题 题型变幻莫测 解析式 勾股定理 抛物线 网易订阅



直角三角形の合同条件
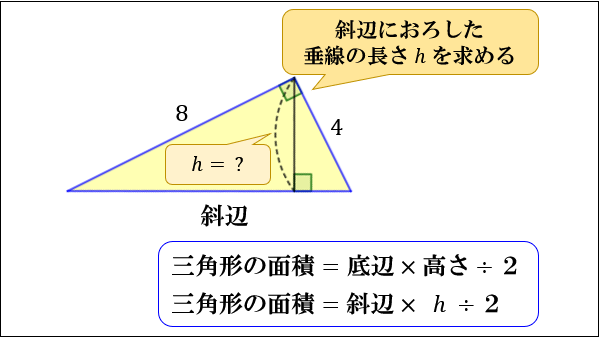



トップ100 正三角形面積小学生 最高のカラーリングのアイデア
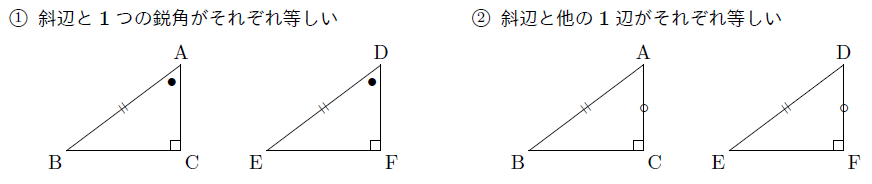



直角三角形の合同条件 まなびの学園
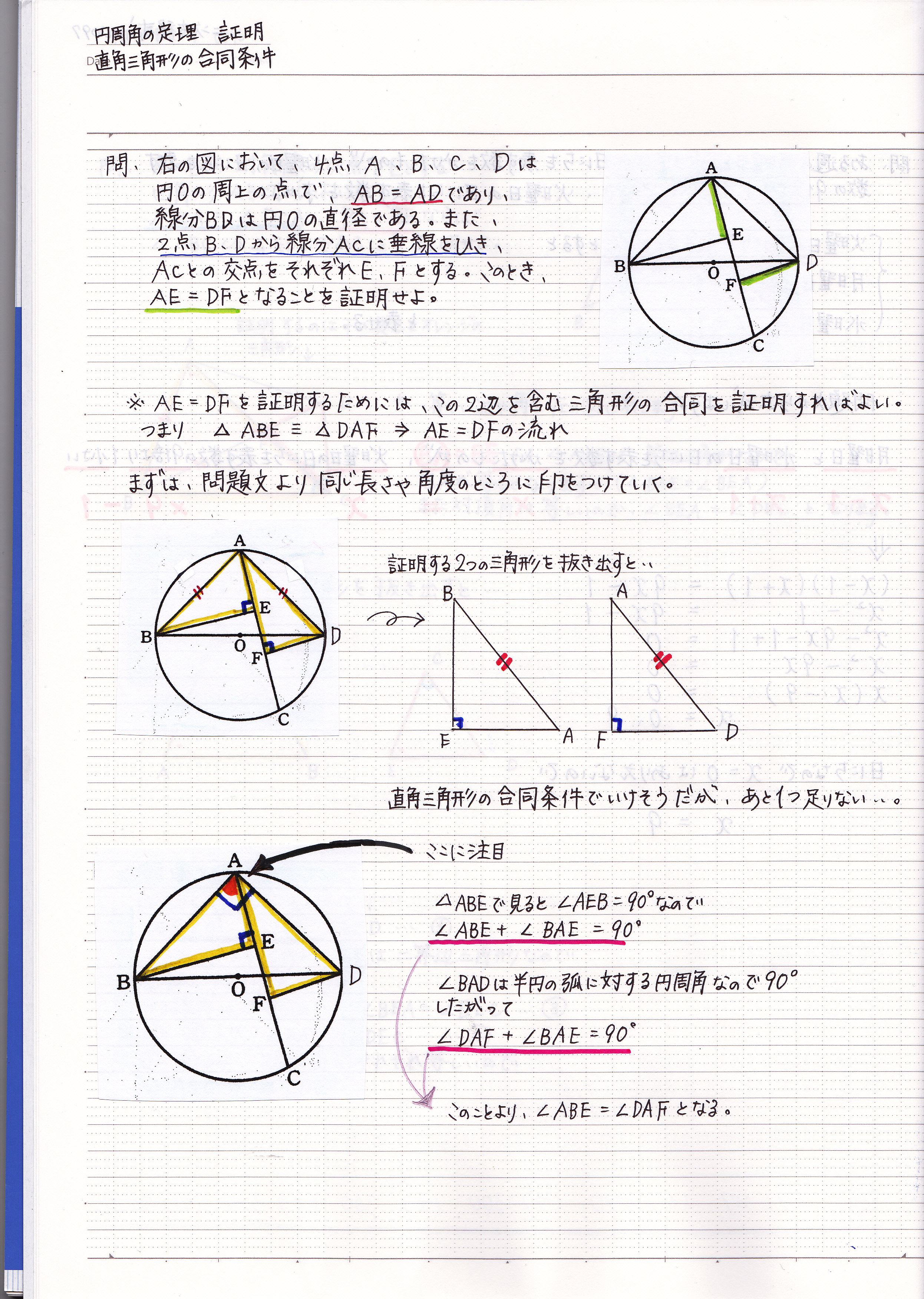



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中2数学 直角三角形の合同条件 例題編 映像授業のtry It トライイット




直角三角形の合同条件 小学生 中学生の勉強




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿