四角錐 ⇒ (上底下底)÷2×高さ 三角錐 ⇒ 底辺×高さ÷2 各図形の底面積の具体的な計算方法を勉強しましょう。※下記も参考になります。 底面積の求め方は?5分でわかる計算、円柱、円錐、四角柱、三角柱の底面積 立方体の底面積四角錐の表面積=底面積 側面積(三角形 つ分) では、実際に問題を解いてみましょう。 次の四角錐の表面積を求めなさい。 (底面は正方形) 展開図を書いて、側面積と底面積を求めると次のようになります。 同じ三角形が4つ分集まって側面になっているので、1つ分の三角形の面積を求めて4倍すると側面積を求めることができますね。 これは底面が正方形三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 立体は切断したり、展開したりしてできる限り平面で考える 直方
1
四 角錐 公式
四 角錐 公式-四面体の体積を求める2つの公式with行列式 レベル ★ 最難関大受験対策; 1辺6の正四面体に内接する球の半径を求めよ。 6 2 1辺16の正方形を底面とする、高さ15の正四角錐に内接する球の半径を




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 体積の求め方、覚え方 体積の公式の覚え方は簡単です。球の体積を除けば、たった2つの公式を覚えるだけで済むからです。基本は柱体の体積(=底面積×高さ)を暗記して、錘体の体積=柱体×1/3④ 角錐や円錐の辺,半径,高さなどを決めて 体積を求める。 準備するもの 模型(四角柱,四角錐,円柱,円錐,など),水,水を入れる容器, 必要に応じて語彙や公式を記したカード Bíw wBíこの公式の証明,および美しい応用としてオイラーの多面体定理の証明を解説します。 → 球面上の多角形の面積と美しい応用 三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators四角すい 四角錐 体積計算 公式 求め方 高さ 底面積 自動 長方錐 方錐 volume 四角錐 体積 面積 四 角錐 体積 公式 四 角錐 体積 公式長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は
三角錐の公式が使えるので、 円錐の体積=底面積×高さ/3 になることがわかります。 (別の例) 上図のように、立方体を考えます。 立方体の中心の点を頂点とし、立方体の1つの面を底面とする図形は 高さが立方体の辺の長さの半分の四角錐です。1 4 9 16 = 30 {\displaystyle { { { {1} {4}} {9}} {16}}=30} 是四角錐数 在 數學 中, 四角錐數 ,或 金字塔數 ,是一個 有形數 表示有多少球堆積成一個 金字塔 ( 四角錐 ,如右圖),這是以 正方形 為基礎( 底面 為 正方形 )。 四角錐數 (square pyramidal number)如右圖所示,第一層第二層第三層第四層每層都是 正方形數 合起來是 正四角錐 ,也就是 正方形數 的級數。 (正四角錐iefghの高さ):(正四角錐iabcdの高さ)= 2:4 (正四角錐iefghの高さ):(正四角錐iefghの高さ) 6 = 2:4 (正四角錐iefghの高さ)= 6 になるね!




100以上四角錐体積公式 ユニークな壁紙サイトhd




50 素晴らしい角錐体積公式 ページを着色するだけ
四角錐台の体積を計算する必要がありました。上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。この様な形の四角錐台を10個作らなければなりませんでした。製作を依頼されて体積がいくらになるかぐらいは理解して製作にかかりたかったのです。計算 四角錐、三角錐、円錐の体積の公式の覚え方(語呂合わせなど)自分流のやり方があったら教えてください! 四角錐 円錐 三角錐 体積 公式 中2 数学 この四角錐の表面積は1cm²。 また底面積=7×7=49cm²であることが展開図よりわかります。 ここで、 四角錐の表面積=底面積+側面積 の公式より 側面積=四角錐の表面積ー底面積=1-49=140(cm²)であることがわかります。 7× ÷2=35 7× =70




高中 B4 1 1 兩面角 四角錐 尹正數學 Youtube
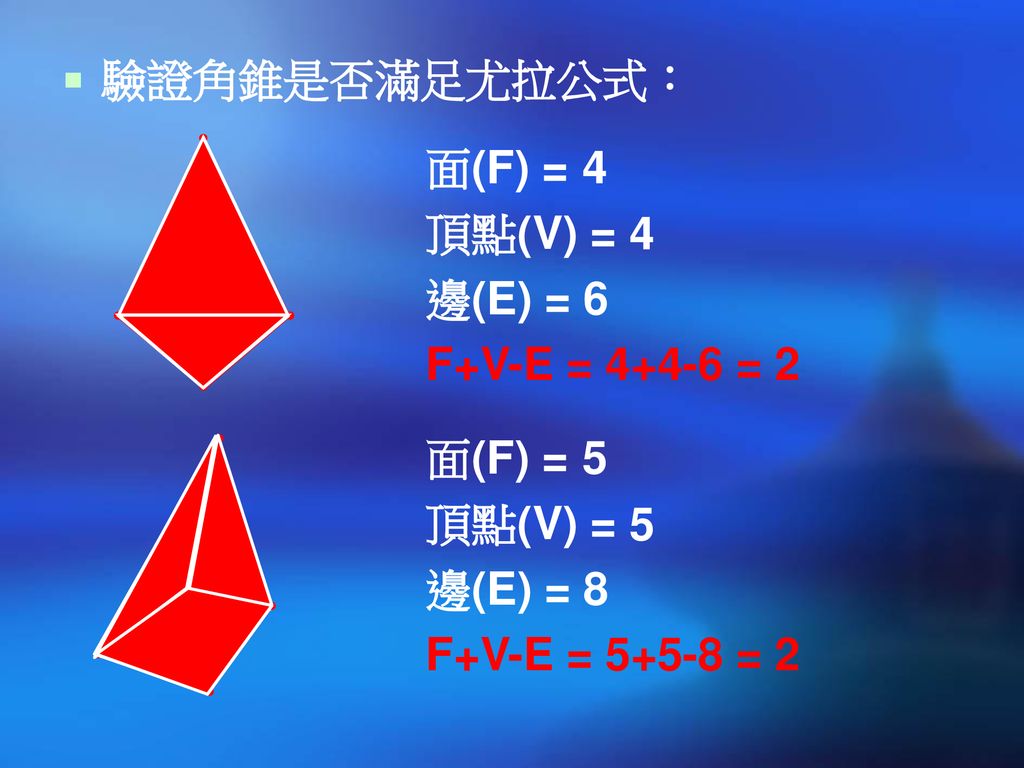



數學黃金講座淺談平面圖形與立體圖形朱峻賢老師 Ppt Download
四角錐 体積 公式 5 底面が正方形で、正四角錐なので、底面の対角線の交点上に高さとなる垂線は下りてきます。, (2) どなたか、簡単な説明方法を教えてください。 ちなみに負かけ正、正かけ負の計算は理解できています。 この問題の円錐の表面積を横 b と d )が並行であり, 高さ h の四角錐台 (稜線は 1 点で交わらなくてもよい) (付図 1) の体積: ④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。四角錐台の体積の公式について。




角錐 円錐の体積と表面積の公式 数学fun




錐體體積公式
出典 フリー百科事典『ウィキペディア(Wikipedia)』 ナビゲーションに移動 検索に移動 1 4 9 16 = 30 は四角錐数 四角錐数 (しかくすいすう、square pyramidal number)は球を右図のように1段目に1個、2段目に4個、3段目に9個、というように 正四角錐 の形に積んだとき、そこに含まれる球の総数にあたる 自然数 である。 つまり 1 から順に 平方数 をいくつかなので、 まずは正四角錐の高さを求めることから始めましょう。 最初に注目するのは底面の正方形です。 このように底面の対角線を引いて、その長さを求めます。 すると45°、45°、90°の直角三角形ができるので の比になりますね。 そこから、対角線の長さは さらに、その半分の長さ まで求めておきましょう。 次に、正四角錐の高さを含む こちらの直角三角正四角錐(辺と高さ) 計算結果:体積、側面積、表面積、側面の高さ、側面の傾斜角 角錐、四角錐台、角錐台、それぞれから各種計算 計算結果:体積 くさび形、正四角錐台、直円錐、円錐台、それぞれから各種計算 計算結果:体積、側面積、表面積




錐體體積公式
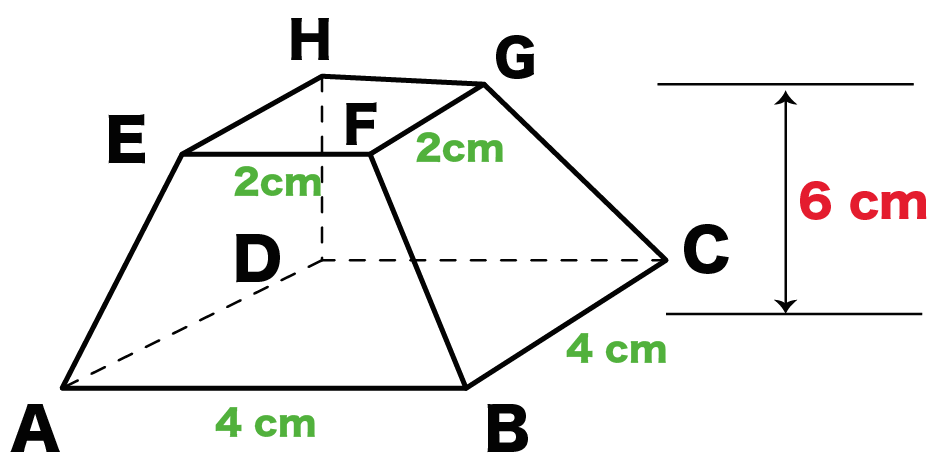



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
角柱(円柱を含む)や角錐(円錐を含む)の体積の公式は、皆さんにとって周知のものだろう。 当HPでも 四面体の求積 三角錐の体積 円柱の体積 直交する円柱 角錐の体積 ある図形の体積 切断面の高さ ・・・ などが話題となり、まとめられてきた。このページでは、立体図形の体積についてただあまり語呂が良くないので、視覚的に「こことここをかけたら側面積になる」という風に覚えるほうが良いでしょう。 また、扇形の面積には一応『 S=1 2 lr S = 1 2 l r 』という公式があり、これを利用したらより簡単に側面積の公式が導けます。 円錐に当てはめると『側面積= 1 2 1 2 ×弧の長さ×母線』です。 『弧の長さ=2×底面の半径× π π 』なので、これを公式 1 四角錐台の体積 上下の底面が長方形で,対応する各辺(縦 a と c;




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




四稜錐 四稜錐是指由四個三角形和一個四邊形構成的空間封閉圖形 而正四稜錐 百科知識中文網
三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。 では次は公式化してみましょう。 今考えていた四角錐の底面は1辺がaの正方形なので、底面積は、 a×a=a 2 ですね。 次に高さは、立方体の半分の高さとなっているので、 a×1/2 です。 したがって、底面積と高さを使って公式をつくるためには、 四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でもないので意味なし



1




球表面積公式球體表面積 百度百科 Kmbymh
でした.これは三角錐でも四角錐でも,円錐でも使える公式です. この式に登場する \(\frac{1}{3}\)って何なの?という話をします. 三角形の面積と一緒?? 上に書いた錐の体積の公式とよく似た形の公式があることに気がつくでしょうか?立体の体積(V),表面積(S)または側面積(F)および重心位置(G) 角錐台 P12 単位換算 公式計算 平面図形の面積(A),周長(L)および重心位置(G) P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 球 P12 球分 P12




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




四角錐の表面積の求め方 公式 小学生 中学生の勉強




優雅四角錐体積公式



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア



圓錐體積公式證明圓錐 Lvnmk



角錐表面積的計算實例 Live 多媒體數學觀念典online



四稜錐 體積公式 體積公式推導 中文百科全書




兩題求看得懂那圖的高人 Clear




四角錐の表面積の求め方 公式 小学生 中学生の勉強
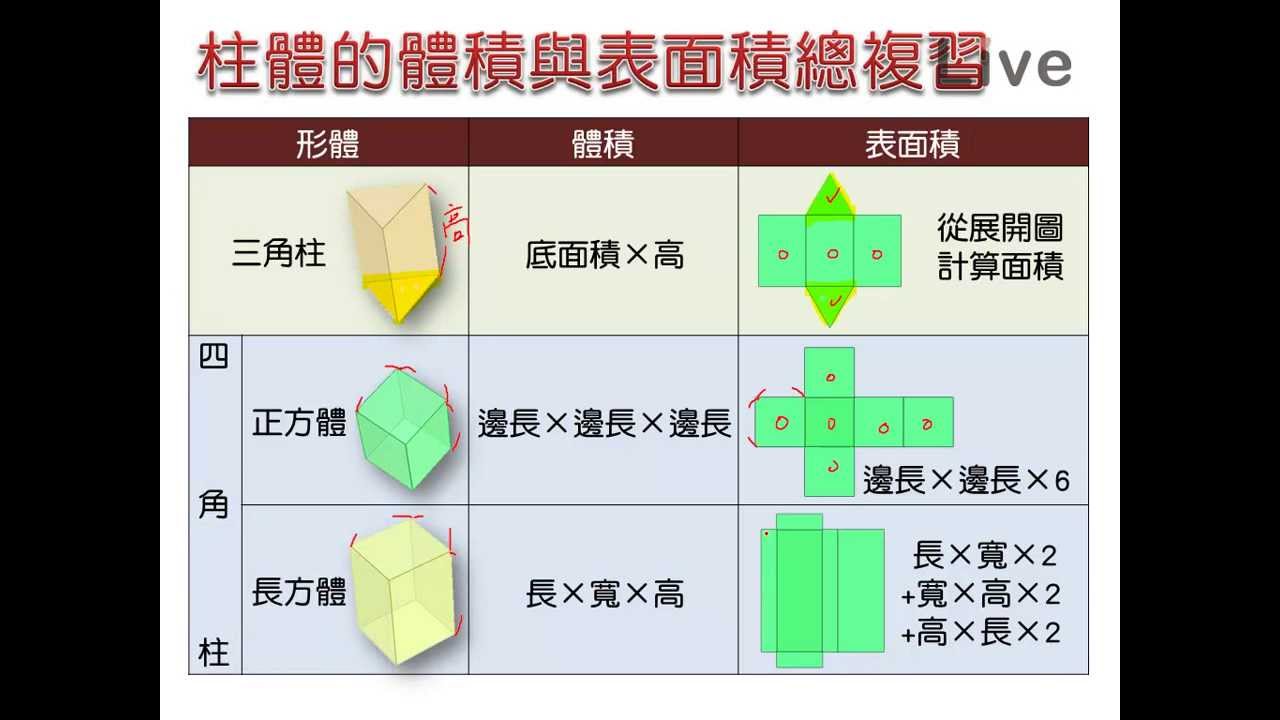



50 素晴らしい角錐体積公式 ページを着色するだけ




長方形面積求邊長翻轉學習影片 國小 數學 3 16 2 Mqttk



平截頭體的體積 Wonder Math
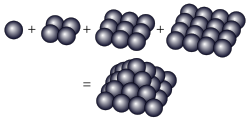



四角錐數 维基百科 自由的百科全书
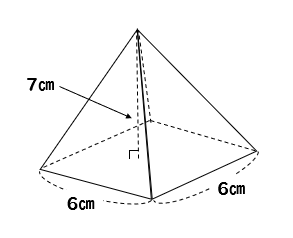



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




四角錐の表面積の求め方 公式 小学生 中学生の勉強




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




優雅四角錐体積公式




四角錐數 维基百科 自由的百科全书



錐體體積公式




四角柱 维基百科 自由的百科全书
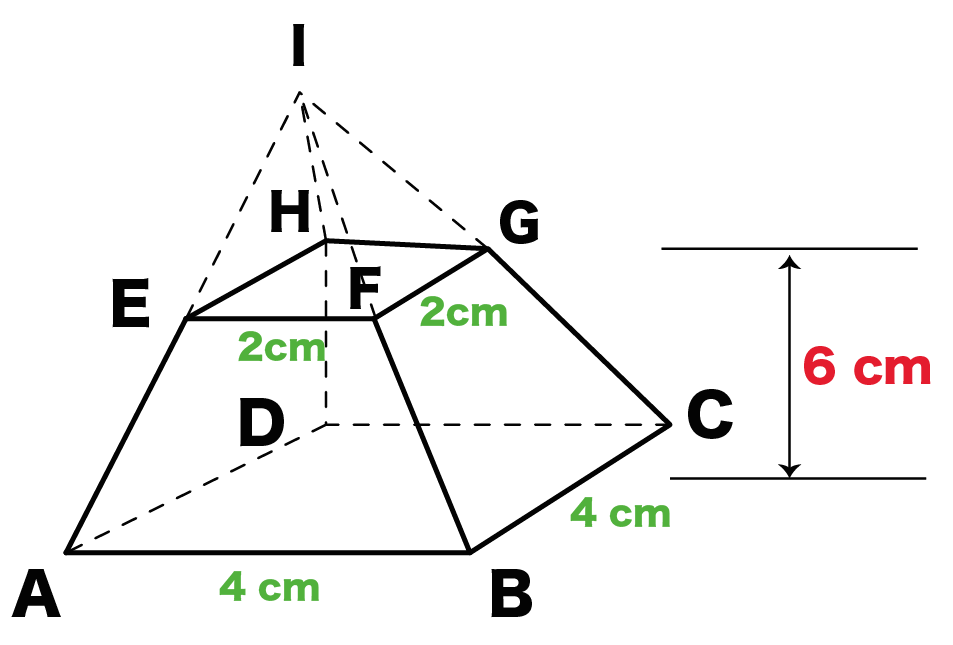



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
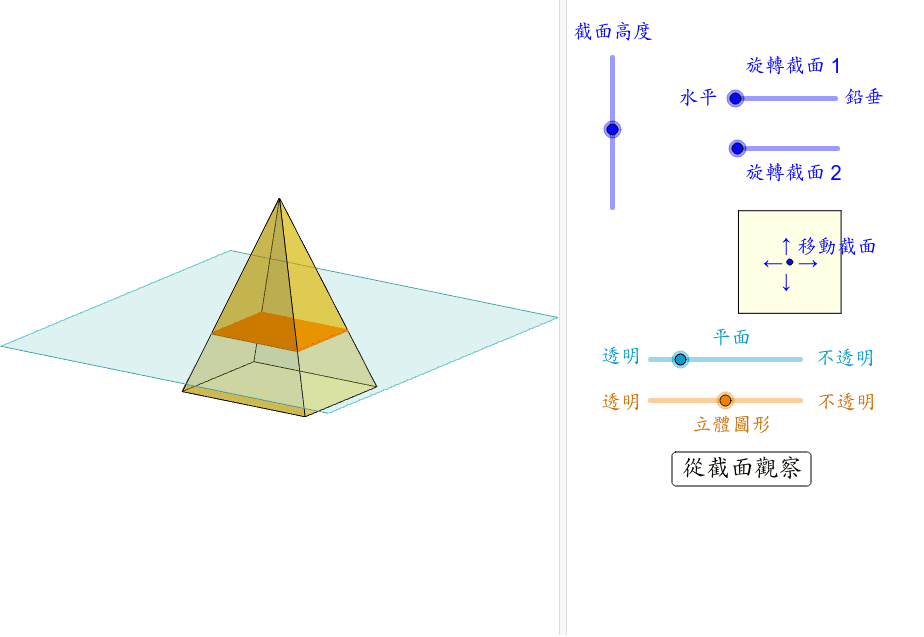



四角錐體的截面 Geogebra




錐體體積公式



数学教育矢量无缝模式与手写公式 任务 情节 计算和几何图形 无尽的质感 手写在版本网格纸上的数学背景库存矢量图 免版税




稜錐 維基百科 自由的百科全書
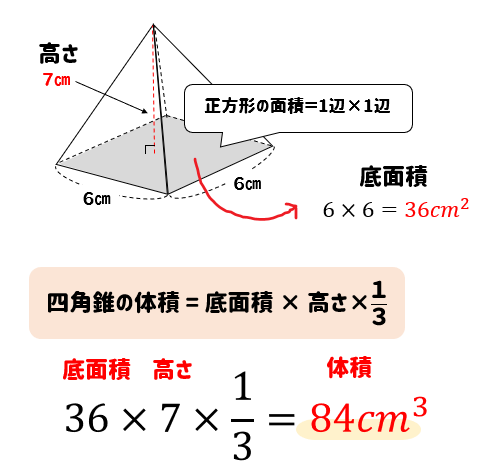



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




角錐體 角錐體是什么 作業幫 Pripdw
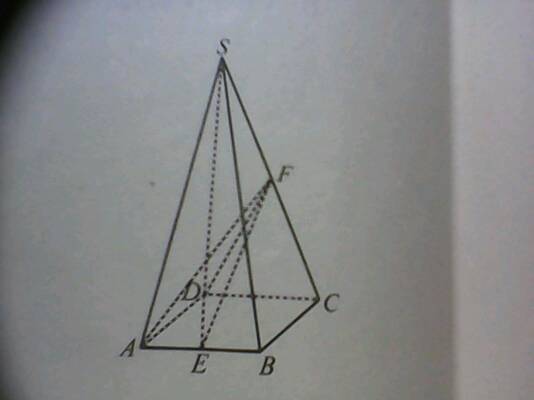



四稜錐 體積公式 體積公式推導 中文百科全書




孩子学习数学思维比背公式重要 每日头条



平行六面體的體積 老王的夢田 痞客邦




基礎 角錐的點 邊 面 Youtube



1000以上四角錐台体積 ニスヌーピー壁紙




四角錐の体積の求め方 公式 小学生 中学生の勉強
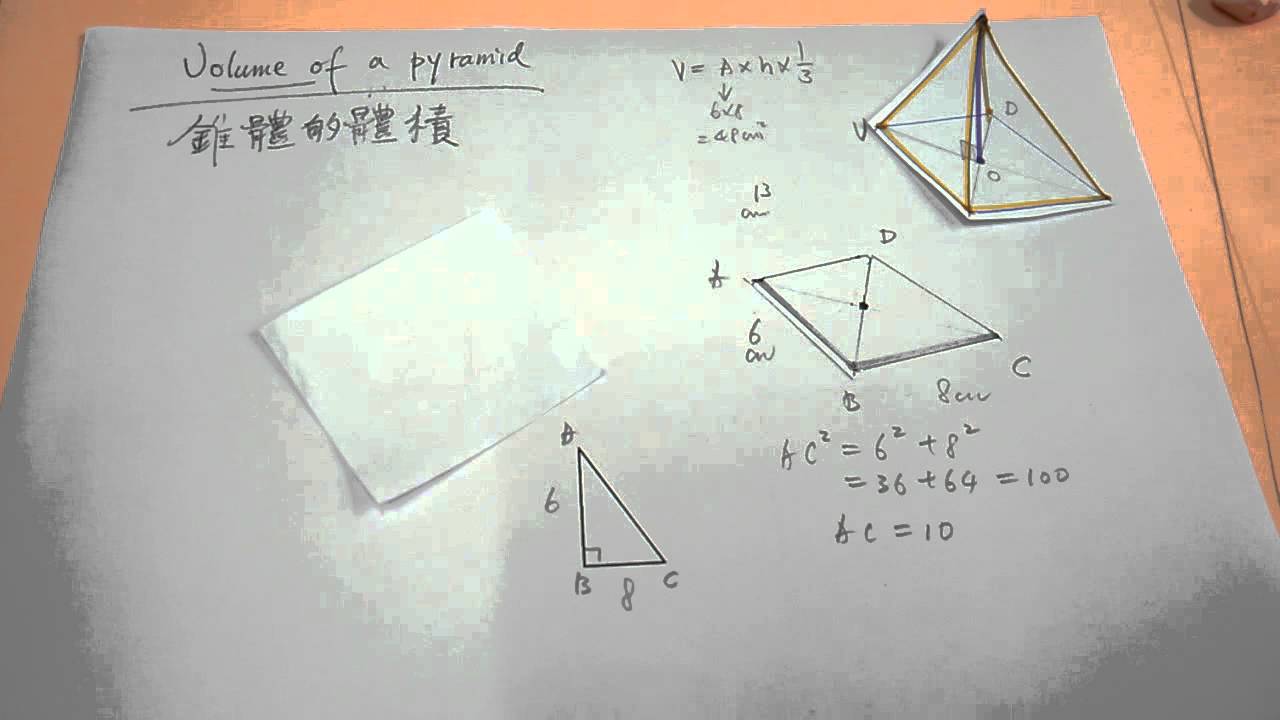



錐體體積 Youtube
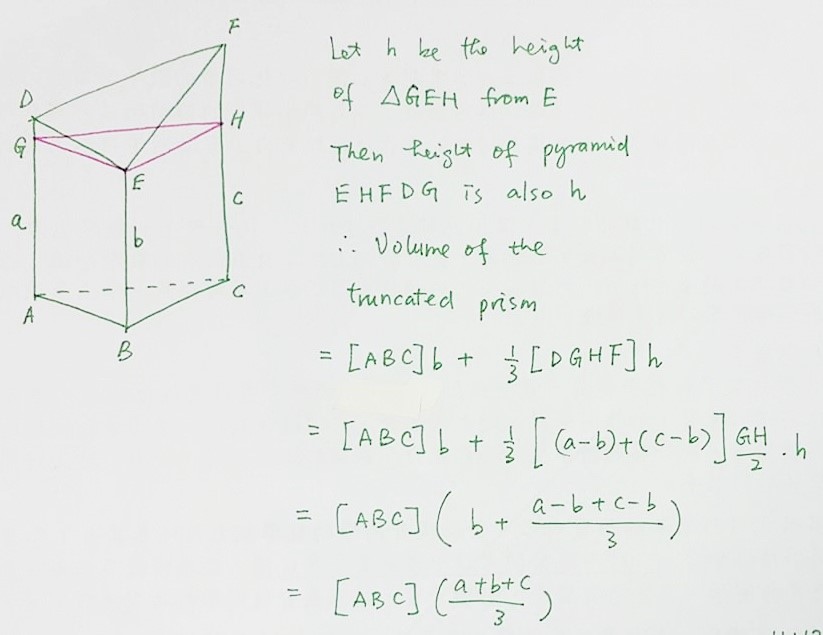



鈄截柱體體積 Quod Erat Demonstrandum




四面體 維基百科 自由的百科全書




如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌



平截頭體的體積 Wonder Math




呈分試攻略 數學科立體圖形概念不清易失分熟讀計算公式提升答題速度 香港經濟日報 Topick 親子 親子資訊 D




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ
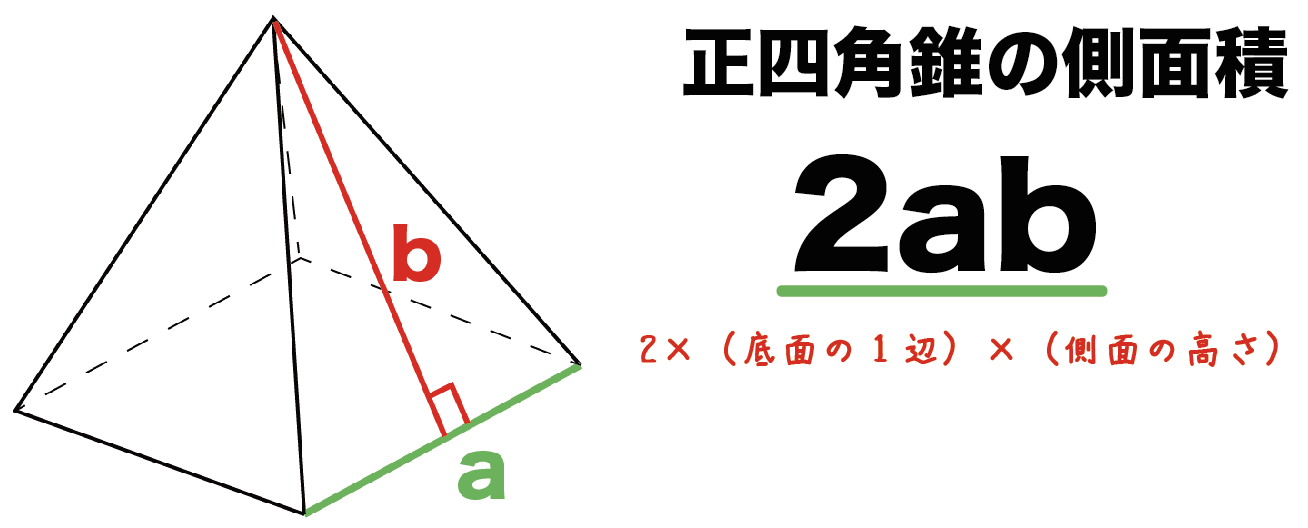



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




數學三角錐公式推導for Android Apk Download




高二空間問題四角錐求高四腳錐求體積金字塔求體積求側面與底面的兩面角餘弦空間問題高二下第一章106龍騰課後卷計算題




圓錐體積公式證明圓錐 Lvnmk




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




锥台 Wikiwand




Topick 新聞 Topick親子 Save低數學必背公式幫助搶分 Facebook




祖氏原理与font Color Red锥体font体积公式费下载下载 Word模板 爱问共享资料
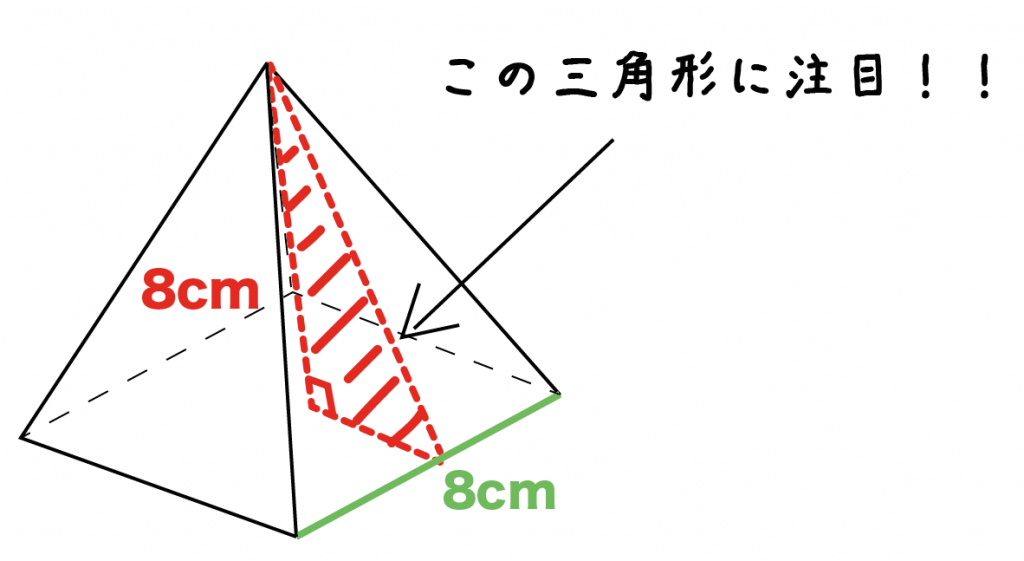



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




50 素晴らしい角錐体積公式 ページを着色するだけ




50 素晴らしい角錐体積公式 ページを着色するだけ




2 1空間慨念
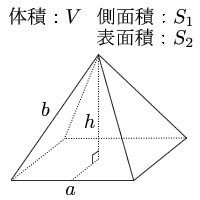



優雅四角錐体積公式



2




角錐體積公式的由來 Youtube



如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌




四角錐の表面積の求め方 公式 小学生 中学生の勉強
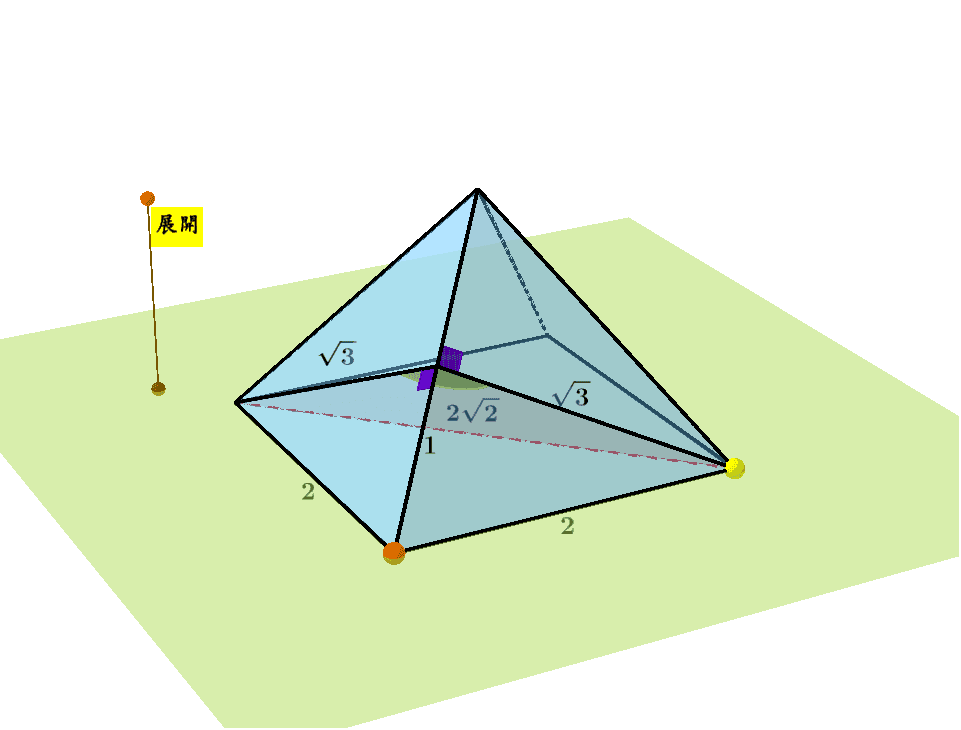



正四角錐兩側面夾角 Geogebra




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特



錐體體積公式




角錐表面積的計算實例 Live 多媒體數學觀念典online




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com
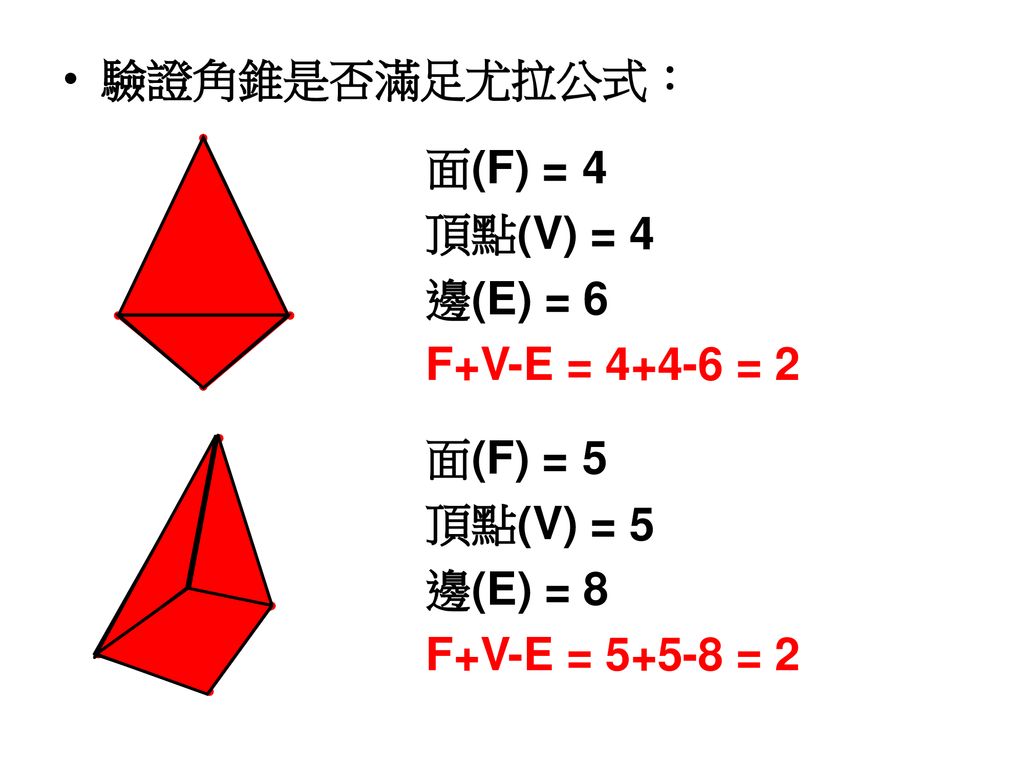



數學講座正多面體莊佳富陳麒任老師 Ppt Download



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
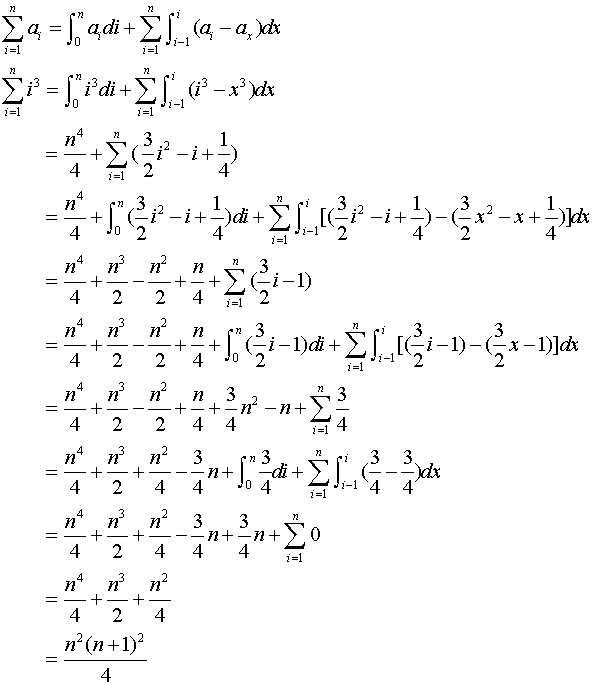



平方和公式 公式 證明方法 中文百科全書



2
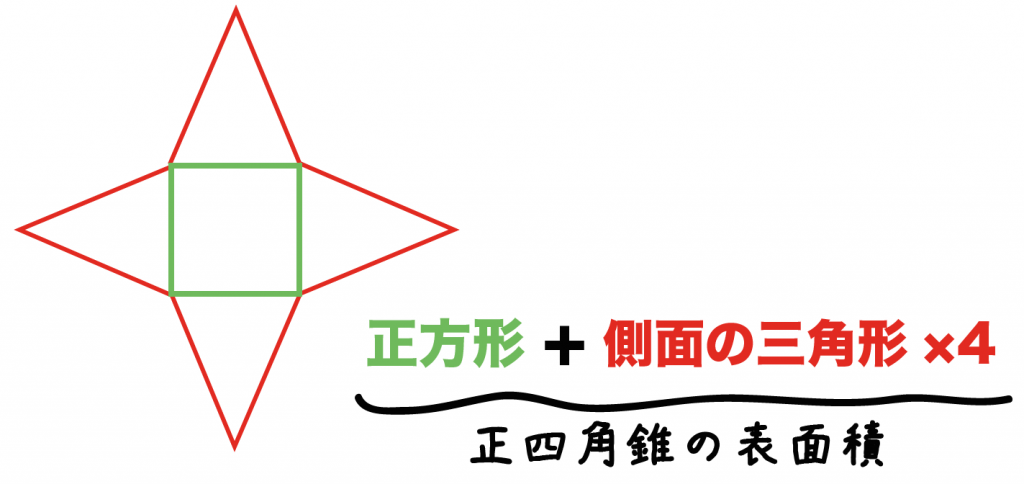



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 正四角錐の体積の求め方がわかる3ステップ マイ勉 0で使える中学生の無料学習サイト 学習 体積 勉強法



1




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
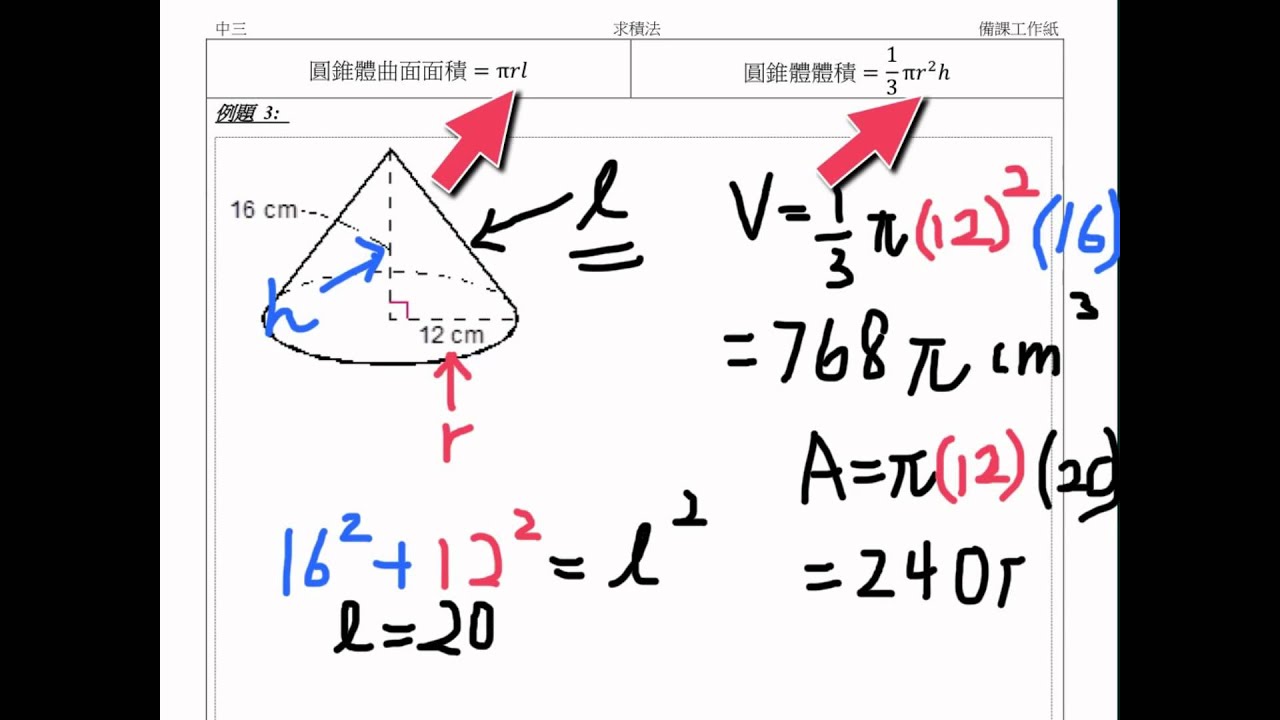



錐體體積 Youtube




球表面積公式球體表面積 百度百科 Kmbymh




正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學 學校沒有教的數學




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




四角柱 维基百科 自由的百科全书




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




錐體體積公式證明




六角錐六角錐數 Yzkgo




トップ100 角錐台体積
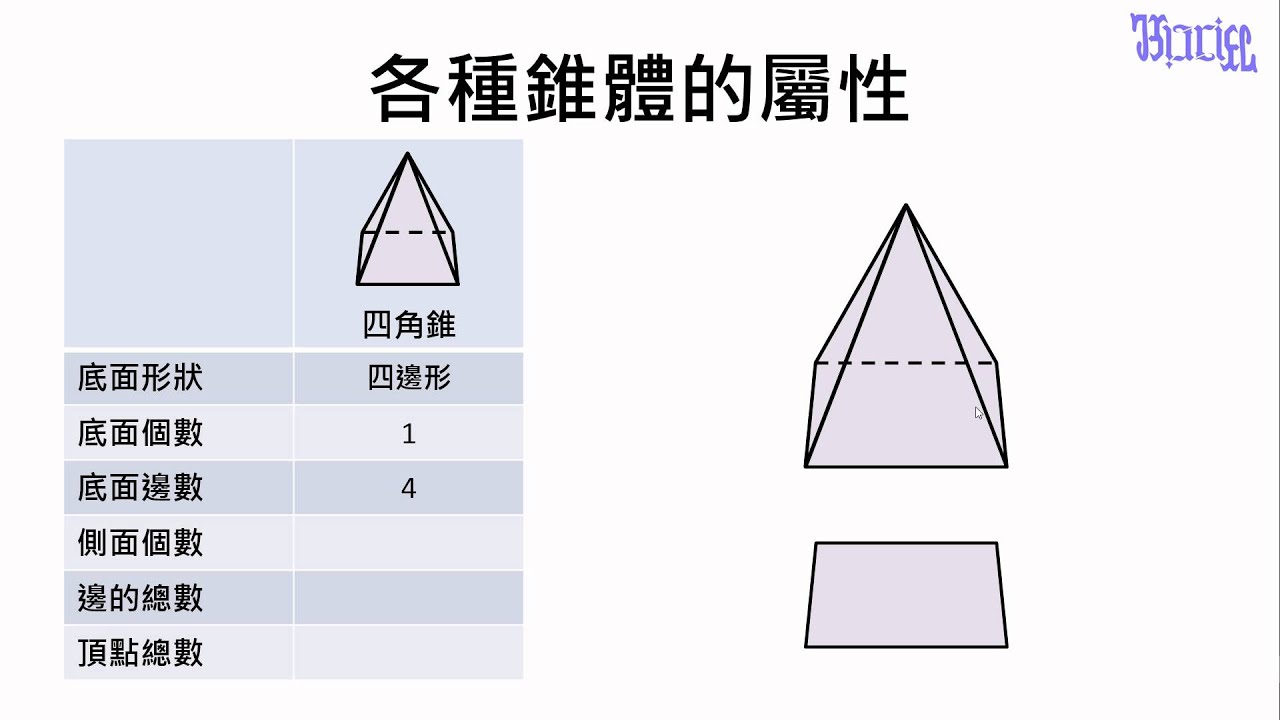



柱體和錐體 16 四角錐的屬性 Youtube




四角錐台の体積 高精度計算サイト



1




體積公式參考 Geogebra
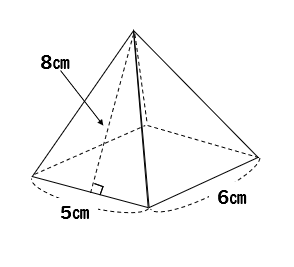



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ
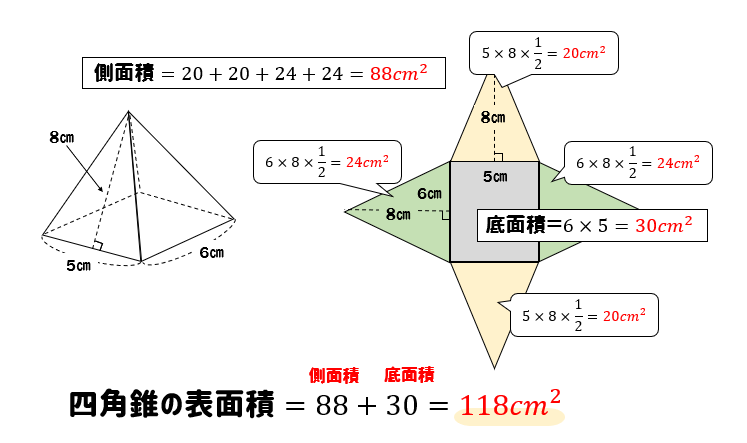



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學 學校沒有教的數學




四面體 維基百科 自由的百科全書




錐體體積公式證明



0 件のコメント:
コメントを投稿