しかしながら、円の面積はまだしも、球の体積、球の表面積の公式となると、その直感的 な把握は難しいようである。 私の周囲の方々に伺っても、「そんなの、鵜呑みにして覚えて、計算したよ~」という場合 が多い。私自身、最初にどうやって教えられ円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデアが出現する。 上野(09)は「測る」というテーマに着目して, 多角形や円の面積,多面体や回転体の体積を求めるた めに必要な極限概念,カヴァリエリの原理,積分概念 などについて論じている。佐伯(13)はN=2 V=πr^2 (円の面積), S=2πr (円周) n=3 V=4/3*πr^3 (球の体積), S=4πr^2 (球の表面積) 4次元以上の球の体積や表面積の計算は、統計力学や量子力学などで使われています。 Sphere in n−dimensional space (1) volume V = πn 2rn Γ(n 21) (2) surface area S = dV dr = 2πn 2rn−1 Γ(n 2) S p h e r e i n n − d i m e n s i o n a l s p a c e ( 1) v o l u m e V = π n 2 r n Γ ( n 2 1) ( 2) s u r f a c e a r e a S =
如何不用微積分算個球 中科院物理所 微文庫
球 表面積 計算機
球 表面積 計算機-半径 r r r の球の表面積は S = 4 π r 2, S=4\pi r^2,\ S = 4 π r 2, 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。 球の体積と表面積の公式を,積分を使って導出します。直径から計算 直径: 体積: 半径から計算 半径: 体積: 球 球 半球 中空球 円周から体積 円柱 円柱 パイプ 円周から体積 立方体 立方体・直方体 角パイプ 錐体 円すい



球冠表面积推导图解 万图壁纸网
球の表面積の求め方 公式と計算例 Scipursuit 表面積の求め方 球 球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。 球的表面積計算公式 球的表面積=4πr^2, r為球半徑 球的體積計算公式 V球=(4/3)πr^3, r為球半徑 阿基米德浮力定律只考慮物體在流體中受到的浮力和重力的作用,其他情況不考慮的! 4 鐺鐺 表面積為4πr² 體積為πr³ 5 M默守快樂 阿基米德浮力定律只能用在靜態使用了二力平衡原理,比如一球の半径(r) 5 2 高さ(h) 3 3 体積(v) =1/3*pi()*b2*(3*b1^2b2^2) 4 側面積(f) =2*pi()*b1*b2 5 表面積(s) =b4 pi()*( 2*b1^2b2^2 ) 6 上面の半径(c) =sqrt( b1^2 b2^2 ) 7 上面積(u) =pi()*( b1^2 b2^2 ) 8 底面積
なので、球の表面積は、 (大円の周の長さ)×(球帯の高さ)= 4πr 2 また 、球冠については次のような驚嘆に値する美しい公式が成り立つ。 エクセルで球の表面積を計算する方法 エクセルで球の表面積を計算する前に、まずその定義について考えていきましょう。 実は級の表面積はその球の半径をrcmとすると、円周率π(パイ:314)を用いると、 表面積=4πr^2cm^2と表現することができます。よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積 $\cross$
体積と表面積 球冠の体積と曲面の面積は、次の値を組み合わせることで計算できる。 球の半径 ;楕円錐台の底面と上面の半軸と高さから体積、側面積、表面積を計算します。 球の体積 球の体積 球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。 表面積を求めるために必要な値は \(r\)(半径)だけですね。 \(r = 4\) を球の表面積の公式に当てはめます。




Avk8t66yhnqn8m




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站
2θで見込む部分の球の表面積の計算 matsubayashi 0748 フォローしました ジャイアントユニラメラベシクル(GUV)などの球体の表面で分子が拡散する場合、どれくらい広がって見えるのか、面積と角度の関係を知りたかったので高校数学に戻って計算。 面積と角度の関係は、下のような感じで S = 2πR^2 (1cosθ) 。 拡散は2次元の拡散で、 = 4Dt で立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例 円錐の立体角は、 $2\pi\left(1\cos\theta_0\right)$ という公式で計算すること球冠,球帯の面積の求め方02 球をある平面で切り取った部分, 球冠 ,の表面積は,以下の図で示すように, 積分範囲を,0からl 2 までにすればよいので, と表すことができます. では,今日を2枚の平面で切り取った部分, 球帯 ,の表面積は....これも積分範囲の指定だけで計算でき,




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org
ところで、本題は「球の表面積・体積」 なんでこんな話をしたかったかというと、球の表面積はイメージするのが難しいからだね。 でも平面に書けちゃうんだったら、イメージできそう。 〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 ということで、 まず半径 の球を、舟形多円錐図法で球の表面積Sおよび体積Vの5秒後の変化率を求めよ。 この問題は微分を用いると、簡単に答えを求めることができます。 ですが、 なんで微分をする必要があるの? という疑問を抱きやすい問題でもあります。 変化率を求めるために、なぜ微分をする必要があるのか。 イチから確認していき球の表面積は 4×円周率×半径×半径=表面積 で求めることができます。 円周率をπ、半径をr、表面積をSとすると、 S=4πr 2 となります。 球の表面積を求める公式



Q Tbn And9gcr4yydsanpcv9odoui8ies6cbemi 5dfwxzcqjdm Pjn0r0 Ymu Usqp Cau




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com
球の体積や表面積と、その球がちょうど入る円柱の体積や側面積との関係を、計算結果等で 確かめ、イメージとしてもっておきましょう。 2( 1 )球の表面積を求める公式: S=4πr2 ( 2)円柱の底面の円の半径: r ,円柱の高さ: 2r (球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積 半球台の体積 円環体の体積 楕円体の体積 一部が欠けた楕円体の体積 一部が欠けた回転楕円体の体積 正多面体の体積 n次元の球の体積球の中心から距離 xの点で切った断面である円の 円周の長さは、L(x)=2π√(r2-x2)となる。 よって、球の表面積Sは、円周をx 方向に積分すると、 S=2∫0r2π√(r2-x2) dxより、 x=rsinθ と置換すると、S=4π∫0(π/2)√(r2-r2sin2θ)rcosθ dθ =4πr2∫0(π/2)cos2θ dθ=4πr2∫0(π/2)(1+cos2θ)/2 dθ =2πr2θ+(sin2θ/2)0(π/2)=π2r2となり、 球の表面積の公式、S=4πr2とは違ってしまう




面积体积计算软件 面积体积计算软件下载v1 0免费版 Pc6下载



球的体积和表面积 比赛稿 图文 百度文库
クラスに対応して,クラス名の付いた class ファイルが出来る. Sample7class を起動することで,Circleclass,Ballclass を動的にリンク (呼び出しの対応付け) して実行を行う. コンパイルと実行の例 (下線部は入力を示す) % dir Sample7java % javac Sample7java % dir Ball球の表面積の計算は,つぎの2つの適用である: 区分求積 長方形の面積の計算公式 いま,半径rの球面を考える: これの面積を,つぎの区分求積で考える: このとき,図のスライスの面積は,ヨコが 2πrcosx でタテが rΔx の長方形の面積で近似される。 この長方形の面積は, 2πr 2 cosx Δx比表面積(ひひょうめんせき、英語:specific surface area)とは、ある物体について単位質量あたりの表面積または単位体積あたりの表面積のことである。 界面に関する学問、界面化学やコロイド化学、あるいは触媒化学などで主に使われる指標である。




球體表面積球體 表面積 體積 Vhjk




3种方法来计算球体的半径
半径 r の球の表面積は、次の式で求められます。 球の表面積 \begin{align*} S = 4\pi r^2 \end{align*} 表面積 = 4 × 314 × 半径 × 半径 公式の導出方法と計算例については、「球の表面積の求め方」をご覧 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための語呂は、面積比法と光束比法による球帯倍数の計算† 専門会員 飯塚 昌之*専 門会員 石野 幸三*・折戸 吉和** 1ま え が き 相互反射に基づく室内全般照明計算法には,照 明率を 表から求めて簡単に概算する場合は別として,計 算によ る場合には,Moonの 誘導した積分方程式による解析解 公式1)や多元連立



球冠表面积计算公式 圣恩灵修网



常用体积计算公式 瑞达电器资料网 华玉生活
円柱の表面積の電卓 URLコピー この電卓は 5724回 使われています 半径 cm mm; 指針:マクをはがして平面にする→面積を計算する 表 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができます. 輪切りの考え方 円柱と球を真横に並べる. 自分の好きな高さで輪切りにする. 輪切りされた部分の表面積(赤まずは、「球の体積」と「球の表面積」を計算する公式の確認をしましょう。 球の体積 半径\(r\)の球の体積\(V\)は $$V = \frac{4}{3} \pi r^3$$ で与えられます(\(\pi\)は円周率) 球の表面積 半径\(r\)の球の表面積を\(S\)は $$S = 4 \pi r^2$$ で与えられます(\(\pi\)は円周率)。



椭球表面积怎么算 作业 慧海网




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站
円柱の体積と表面積を求めるクラス。 15~28行目 円錐の体積と表面積を求めるクラス。 29~39行目 球の体積と表面積を求めるクラス;球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume 球の体積 面積;大さじ1杯が15ccということは知っていましたが、この中に1辺1cmのキューブが15個も入るのが実感できなくて計算してみました。 10 1524 30歳代 / 会社員・公務員 / 非常に役に立った /




用感覺理解球體表面積公式 Youtube



球体表面积公式 怎样计算球体的表面积
よって,球帯の表面積は S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ S=2\pi r^2\int_{\theta_1}^{\theta_2}\cos\theta d\theta S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ (ただし, θ 1 \theta_1 θ 1 は球帯の底面の緯度, θ 2 \theta_2 θ 2 は球帯の天面の緯度)43~48行目 変数を宣言。 entyu==円柱 ensui==円錐 kyu==球 tai==体積 men==表面積 を表している。 50~52行目公式計算 平面図形の面積(A),周長(L)および重心位置(G) P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 球 P12 球分 P12 球欠 P12 球帯(a・b・h) P12 球帯(a・b・r) P12 角柱 P12 角錐



椭圆球表面积公式球体表面积公式




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科
青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおく. この薄い球殻を集めると球体が完成する. 計算 球体の体積は なので 両辺



Q Tbn And9gctgcict9gm0gtufwk9tgukjgjcvgg71cjlzzvman6pfcoke0xwb Usqp Cau




球表面積公式球體表面積 百度百科 Kmbymh




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科




體表面積表初中數學 幾何 面積與體積公式 Uhlwc



写给5年级的学生 球公式是如何推导出来的 表面积



球的表面积公式 球的表面积公式画法



球的体积公式 万图壁纸网



球冠表面积推导图解 万图壁纸网




如何计算球的体积 5 步骤




球體表面積球體 表面積 體積 Vhjk




球體積的前世今生 每日頭條



高中数学第一章空间几何体1 3空间几何体的表面积与体积2球的体积和表面积 教案 新人教a版必修2 Doc 课件巴巴kejian Com 课件巴巴kejian Com




椭球表面积计算器下载1 0 绿色版 椭球表面积公式 Pc6下载




球の体積と表面積 公式と計算問題と証明 Irohabook




Java计算圆锥体积 如何求球的体积与表面积 五犬的博客 程序员宅基地 程序员宅基地



球体表面积公式 100查分网




球剖体积的计算公式 一个球半径为1 3 沿一半径30厘米处做一剖面 求球体被切后剩下部分的体积 三人行教育网 Www 3rxing Org




60分 童生段学生 计算长方体外接球表面积 知乎



圆球表面积公式推导球体的体积公式 表面积公式的推导



Search Q E5 9c 93 E9 8c 90 E9 Ab 94 E9 Ab 94 E7 8d Tbm Isch



球体计算公式大全 西瓜视频搜索




6 1 3面积和体积公式 第1课时 棱柱 棱锥 棱台和球的表面积学案 含答案 七七文库www 77wenku Com




球表面積公式球體表面積 百度百科 Kmbymh




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站




球体表面积



球表面积公式推导图解 搜狗图片搜索




Python求体积 Python计算圆柱体表面积 用python计算圆的面积



如何不用微積分算個球 中科院物理所 微文庫




球的表面积公式 球的表面积公式画法



立体图形的表面积和体积的计算方法及公式 立体图形的表面积和体积 奥数网



外接球表面积 哔哩哔哩 つロ干杯 Bilibili




通過變量計算球體體積和表面積 每日頭條



1 球体计算公式2 球缺计算公式 尚书坊



空间几何体的表面积和体积球 柱 锥 台的表面积和体积的计算公式及其应用下载 Word模板 爱问共享资料



球体的表面积体积计算公式是什么 尚书坊




胶囊罐体 球冠高等于柱体半径 体积 表面积计算公式 三贝计算网 23bei Com




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



腾讯视频




球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客 球缺的表面积计算公式




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站



椭球表面积计算器下载v1 0绿色版 附带椭球表面积公式 多多软件站




球體積計算球體體積計算器 Rkdof
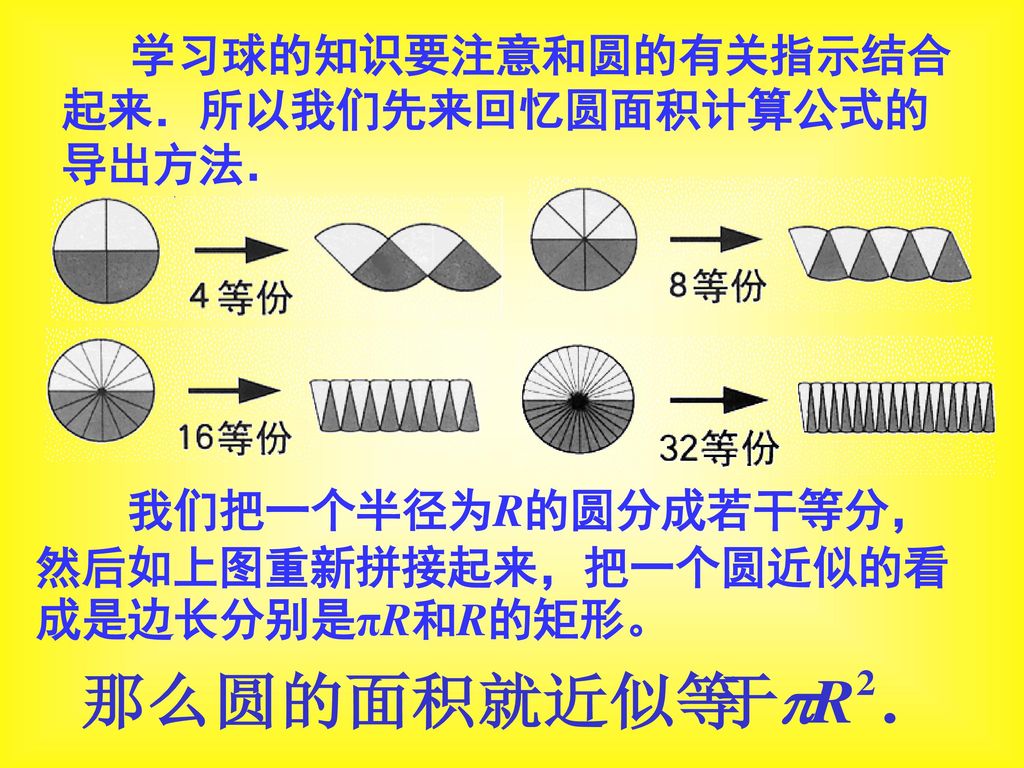



球的体积和表面积ppt Download




球体的表面积和体积的计算公式 星火网校




球體表面積及體積的推導 每日頭條
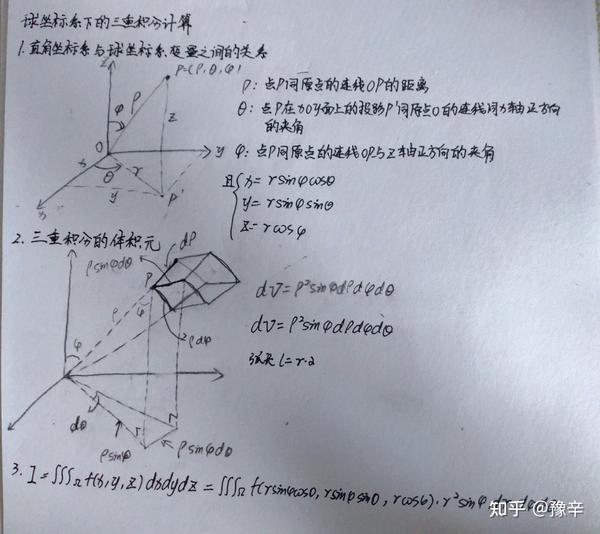



三重积分求球的表面积 用积分求球的表面积 用重积分计算球的表面积



球体的表面积体积计算公式是什么 尚书坊



Http 163 25 96 19 107first Program Hw Hw5 Hw5c Pdf




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



椭球表面积计算器下载 椭球表面积公式计算下载v1 0 绿色版 It猫扑网




球表面積公式球體表面積 百度百科 Kmbymh



圆球表面积 球体表面积的公式证明 篆体字转换器




表面積怎麼算考綱原文了解球 稜柱 稜錐 臺的表面積和體積的




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com




高考数学考点之空间几何体的表面积和体积 王羽课堂



表面积计算公式比表面积定义公式 所有表面积公式




8 3 三重积分的计算part 5 球坐标系下三重积分的计算 Youtube




21一轮复习丨必修一球的体积和表面积 人人焦点



1




球缺 一個球被平面截下的一部分叫做球缺 截面叫做球缺的底面 垂直于截面的直徑被截下的 華人百科
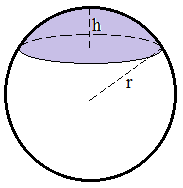



球冠体积 表面积在线计算器




球的表面积计算公式球的表面积与体积计算公式 学习问题 100教育家长学院



球的表面积计算公式 扒拉扒拉




7ypmx8vhpydmgm



1 球体计算公式2 球缺计算公式 尚书坊




圆环体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球體的體積球體 360百科翻譯此網頁 Gahzw



18届高考数学一轮复习第七章立体几何第二节空间几何体的表面积 与体积学案 文科 Doc 课件巴巴kejian Com 课件巴巴kejian Com




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



圆球体积计算公式球体积公式球的体积计算公式为43pr3 求半径为3 5cm的球的体积 P取3 14 结果保留五个有效数字 爱华网




22高三数学第一轮复习 空间几何体的表面积与体积公式大全 升学 恒艾教育
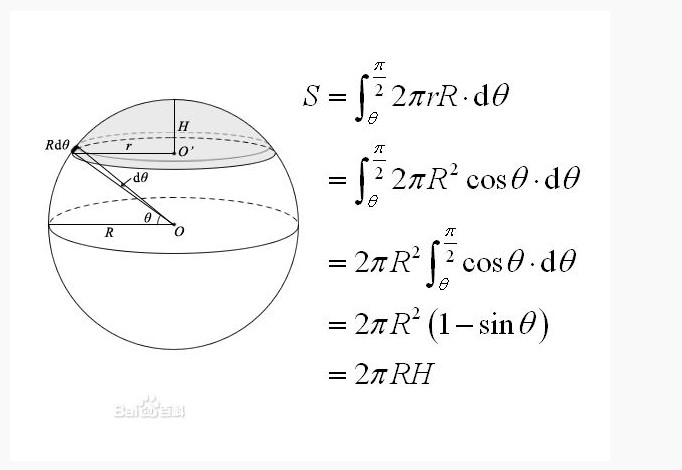



球冠表面積公式 計算方法 注意事項 中文百科全書



椭球表面积计算器下载 椭球表面积公式计算版1 0 系统之家



数学一分钟球的表面积公式推导证明 哔哩哔哩 Bilibili



球的表面积公式 球的表面积公式画法



不锈钢球体的表面积计算公式讲解 温州钧达阀门球体有限公司



两类特殊椭球缺的体积与表面积 文档库



圆球表面积计算器
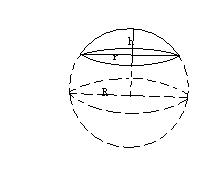



球缺 维基百科 自由的百科全书



球的表面積的求法 中學數學課 隨意窩xuite日誌



细品教材 从生活经验中我们知道 不能将橘子皮展成平面 因为橘子皮近似于球面 这种曲面不能展成平面图形 那么 人们又是怎样计算球面的面积的呢 古人在计算圆周率时 一般是用割圆术 即用圆的内接或外切正多边形来逼近圆的周长 理论上 只要圆内接正多边形边




油罐拱顶面积怎样计算 油罐拱顶表面积计算公式表达式底面积 35 784 拱高 0 739 求拱的表面积 三人行教育网 Www 3rxing Org




球體表面積球體 表面積 體積 Vhjk



球的体积与表面积计算公式的推导 哔哩哔哩 つロ干杯 Bilibili




头条文章
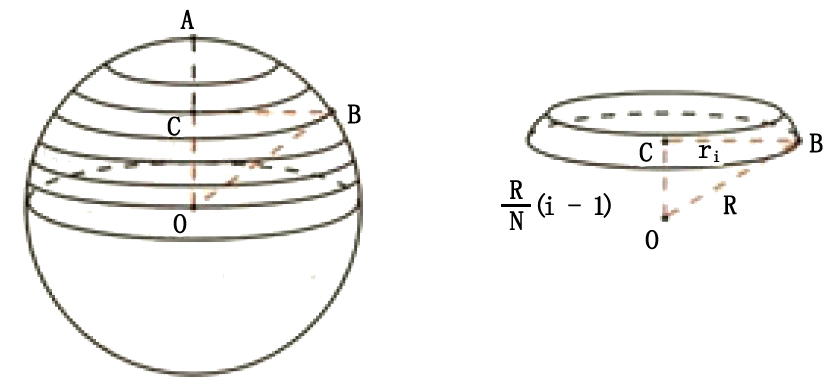



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客



0 件のコメント:
コメントを投稿