Examples • The graph of f(x)=x2 is a graph that we know how to draw It's drawn on page 59 We can use this graph that we know and the chart above to draw f(x)2, f(x) 2, 2f(x), 1 2f(x), and f(x) Or to write the previous five functionsNpressions Kon of Example 2 The graph of y=f(x) is given below Refer to it to sketch the others 5 y = f(x) y = 3f(x) ATP a va son Oh VeSAN y=f(x) y=2f(x 2 LA An invariant point is one that is unaltered by a transformationFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
Graphing Quadratic Functions
Y=f(x) graph examples
Y=f(x) graph examples-If (x, y) belongs to the set defining f, then y is the image of x under f, or the value of f applied to the argument x In the context of numbers in particular, one also says that y is the value of f for the value x of its variable, or, more concisely, that y is the value of f of x, denoted as y = f(x)Then the graph of y = f (x) is obtained by reflecting the graph of y = f (x) across the y


Graphs Of Functions
Example We have a function \(y = f(x)\) We have multiplied the function with 2, ie, \y = 2f(x)\ We get, The distance of the points on the curve gets farther away from the xaxis The shape of the curve depends on the value of C If C > 1, the graph stretches and makes the graph steeper If C < 1, the graph shrinks and makes the graph flatterSep 23, 01 · Relative to a hyperreal extension R ⊂ ⁎ R of the real numbers, the derivative of a real function y = f(x) at a real point x can be defined as the shadow of the quotient ∆y / ∆x for infinitesimal ∆x, where ∆y = f(x ∆x) − f(x) Here the natural extension of f to the hyperreals is still denoted f Here the derivative is said to exist if the shadow is independent of the infinitesimalOct 19, · Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign up
Apr 12, 18 · For example, the graph of the function \(f(x)=x^34\) is the graph of \(y=x^3\) shifted up \(4\) units;Remember f(x) reflects any part of the original f(x) graph that was below the xaxis in the xaxis In this video I show you how to draw graphs of the form y=f(x) using the modulus function and give you three graphs to try Examples in the video Sketch the following ySo let's start with the function f of x =4x I'm going to graph that function and then I want to graph f of 4x So let's make this our parent function it's actually pretty easy to come up with values for it and you know what the shape is going to be, it's a radical function
Therefore, every coördinate pair on the graph of that function is (x, y) = (x, x 2) The ycoördinate is x 2 In other words, the graph of a function y = f(x) is that geometrical figure such that every coördinate pair on it is (x, f(x)) The ycoördinate is f(x) For example, if y = f(x) = x 1, then every coördinate pair on its graphThe statement Y=f(x) in this example will refer to the proven x's determined through the steps of a Six Sigma project Advance Your Career, Enhance Your Skills Get Six Sigma Certified Today!Well instead of flipping the y values, you want to flip the x values So you replace the x with minus x and that will reflect the graph across the y axis So let's consider an example y=2 to the negative x This is a reflection of what parent function?
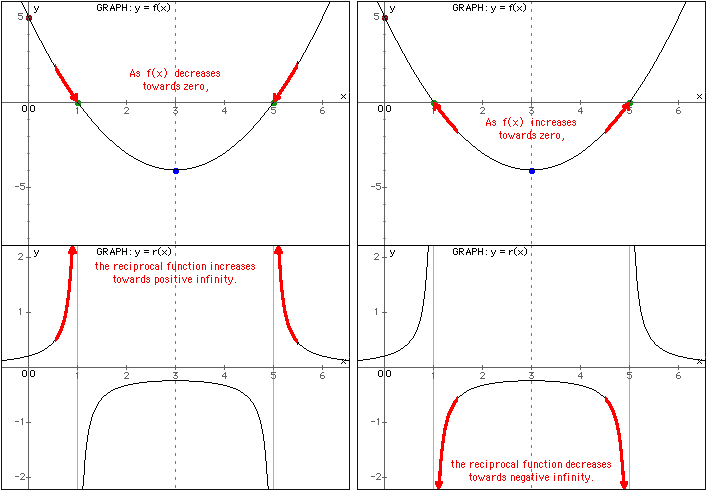


Asymptote


Introduction To Exponential Functions
Inverse Functions An inverse function goes the other way!I want to know what's the transformation y=f of bx do?The following table gives a summary of the Transformation Rules for Graphs Scroll down the page for more examples, solutions and explanations Function Transformations Horizontal And Vertical Translations This video explains to graph graph horizontal and vertical translation in the form af(b(xc))d It looks at how c and d affect the graph



Day 6 Examples U3f13


Transformations Mrs F X
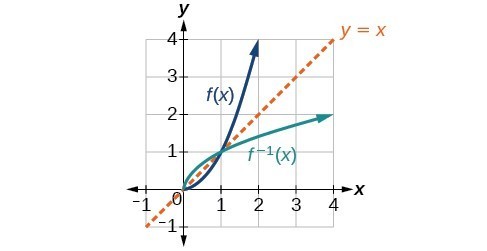
Answer to The graph of y = f(x) passes through the points (1, Transcribed image text The graph of y = f(x) passes through the points (1, 4) and (3,8) The tangent line to y = f(x) at (3,8) has the equation y = 3x 17This problem solving methodology takes you through the process of determining all potential "x's" that influence on time deliveries and then determiningF (x) = x3 Let y = x3 Let us find the inverse function, for that we have to solve for x x = y1/3 Now we have to replace "x" by "f1(x)" and "y" by "x" f1(x) = x1/3 By finding inverse of the given function, we get the other function Note The graph of y = f−1(x) is the reflection of the graph of f in y = x



Ch 3 1 3 2 Functions And Graphs
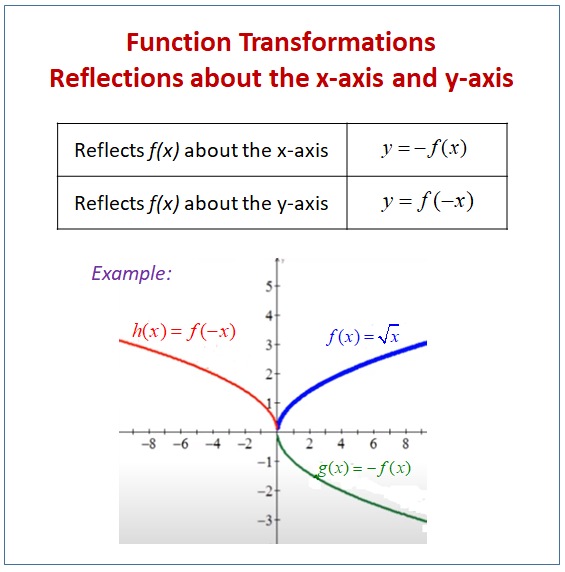


Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities
Jun 09, · Example 1 Graph the logarithmic function f(x) = log 2 x and state range and domain of the function Solution Obviously, a logarithmic function must have the domain and range of (0, infinity) and (−infinity, infinity) Since the function f(x) = log 2 x is greater than 1, we will increase our curve from left to right, a shown belowAug 14, 18 · Simply put, the Y=f(x) equation calculates the dependent output of a process given different inputs Here's an example of some possible values for the variables in the "breakthrough equation" In a marketing context, the outcome (Y) could equal the number of product sales, where the function (f) could be email opens from a newsletter campaign, and the input (x) could be theY=f of x flips the graph across the x axis But how do you reflect it across the y axis?



Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
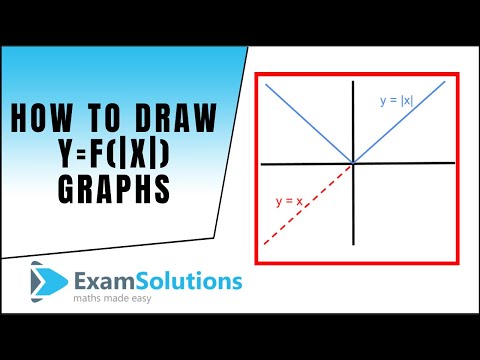


Graphing Y F X Examsolutions
The graph of f(x) in this example is the graph of y = x2 3 Choose a value for the first coordinate, then evaluate f at that number to find the second coordinate following table shows several values for x and the function f evaluated at those numbers Each column of numbers in the table holds the coordinates of a point on the graph of fApr 26, 17 · Given the graph of a function \(y=f(x)\), we can sketch an approximate graph of its derivative \(y=f'(x)\) by observing that heights on the derivative's graph correspond to slopes on the original function's graph In Activity 110, we encountered some functions that had sharp corners on their graphs, such as the shifted absolute value functionExplain how the graph of the function compares to the graph of y = f(x) For example, for the equation y = 2(x 3), the graph of fis shifted 3 units to the left and stretched vertically by a factor of 2 y = 5f(x 8) The graph off is shifted 8 units to the left and compressed vertically by factor of


Graphing Quadratic Functions
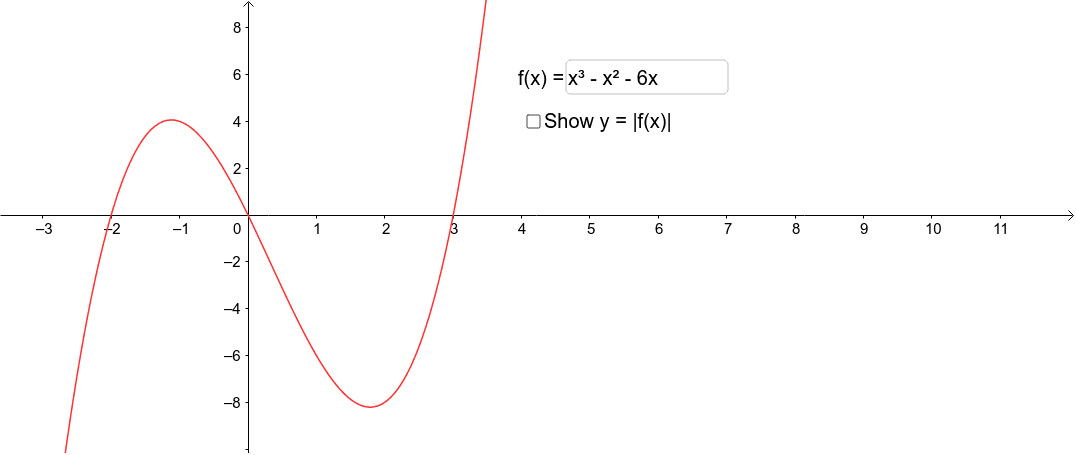


The Graph Of Y F X Geogebra
The parameter a can be added to or subtracted from the input x before the rule f is applied y = f(x) becomes y = f(x ± a) These transformations are called horizontal shifts or translationsThey move the graph of the given function left (adding positive a) or right (subtracting positive a)Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;Reflection of Graph The graph of a given function can be reflected around {eq}x {/eq}axis (vertically) and {eq}y {/eq}axis (horizontally) If the function is given as {eq}y = f\left( x \right


If The Minimum Point On The Graph Of The Equation Y F X Is 1 3 What Is The Minimum Point On He Graph Of The Equation Y F X 5 How Would I Go Enotes Com
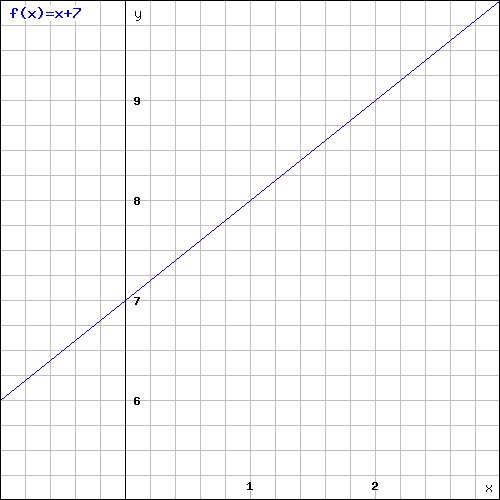


Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet
When I think of y=f(x), i Think of y = f(x)= 1, x = 1, x =2, then y =f(x) =2, x =3, then y= f(x)=3, and so on Hi John, I find it helps sometimes to think of a function as a machine, one where you give a number as input to the machine and receive a number as the outputSpecify a function of the form y = f(x) The function must accept a vector input argument and return a vector output argument of the same size Use array operators instead of matrix operators for the best performance For example, use * (times) instead of * (mtimes)Float Y = f (float X) where f calculates the result in the correct dimensions, then casts it to float auto function_3K = (float x) { /* first transform xcoord into wavelength / µm */ long double wavelength = long double (x) * Micro ();



Graph Of Y X And Y F X In Example 9 Download Scientific Diagram



Draw Graph Of Frac 1 F X From Graph Of F X Mathematics Stack Exchange
The graph of y = f (x) is shown in the xyplane What is the value of f (0)?The equation For example the graph of the equation x2 y2 = 1 is the unit circle (circle of radius 1 centered at the origin)10 05 05 05 10 x 2y =1 If we can solve for y uniquely in terms of x in the given equation, we can rearrange the equation to look like y = f(x) for some function of xView MATH10E_Examples_and_graphspdf from MATH 10 at The Chinese University of Hong Kong MATH10E Advanced Calculus I Examples and graphs Figure 1 Caption This is the graph z = f (x



Example Of Area Bounded By Graph Y F X And Limits X A X B And Download Scientific Diagram
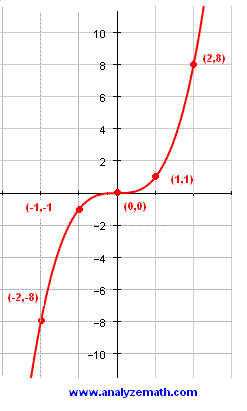


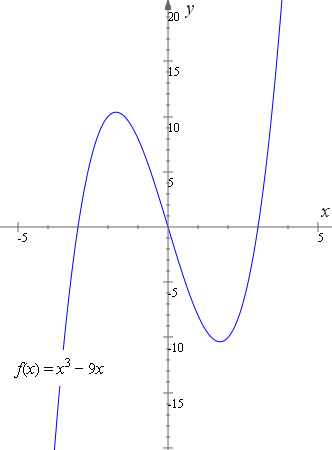
Graphing Cubic Functions
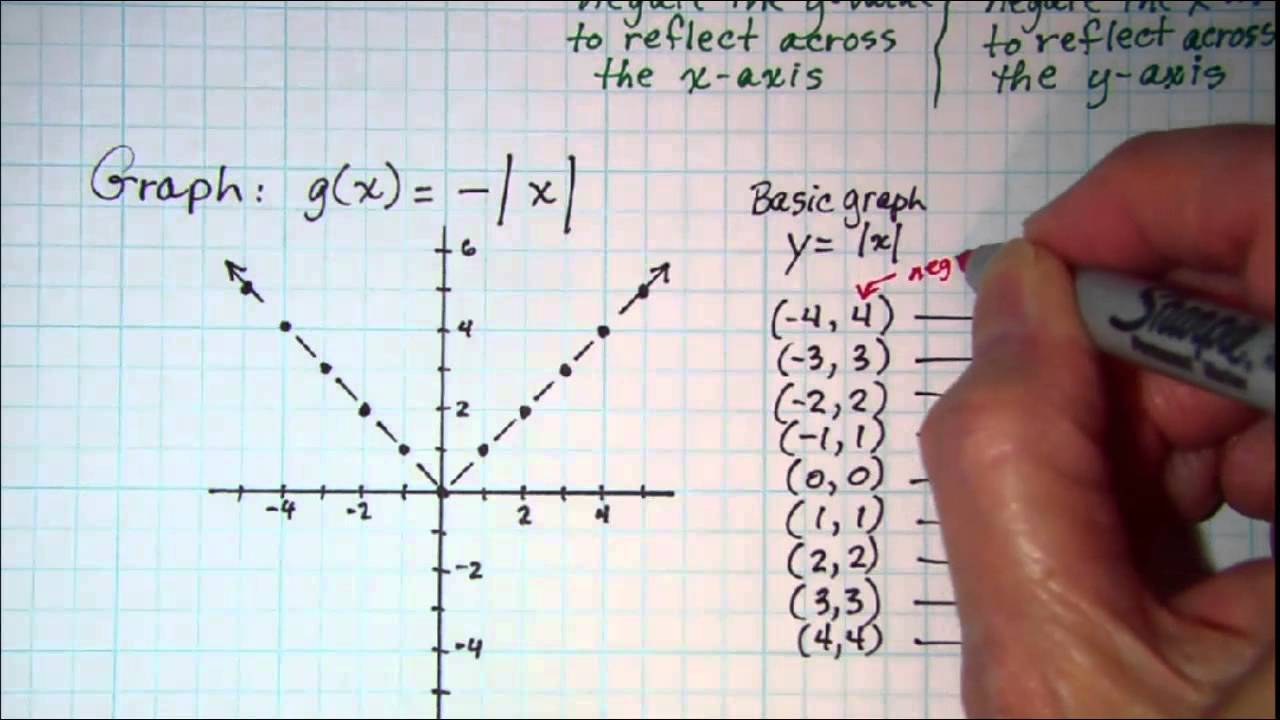
The equation of the reflection of f(x) about the yaxis is y = f(−x) Example 2 Sketch the graph of y = −x 2 x 6 Solution It is best to consider a graph when the leading coefficient is positive Therefore, let us call the given functionLet us start with an example Here we have the function f(x) = 2x3, written as a flow diagram The Inverse Function goes the other way So the inverse of 2x3 is (y3)/2Jul 15, 11 · In this video I try to explain what a function in maths is I once asked myself, why keep writing y=f(x) and not just y!??
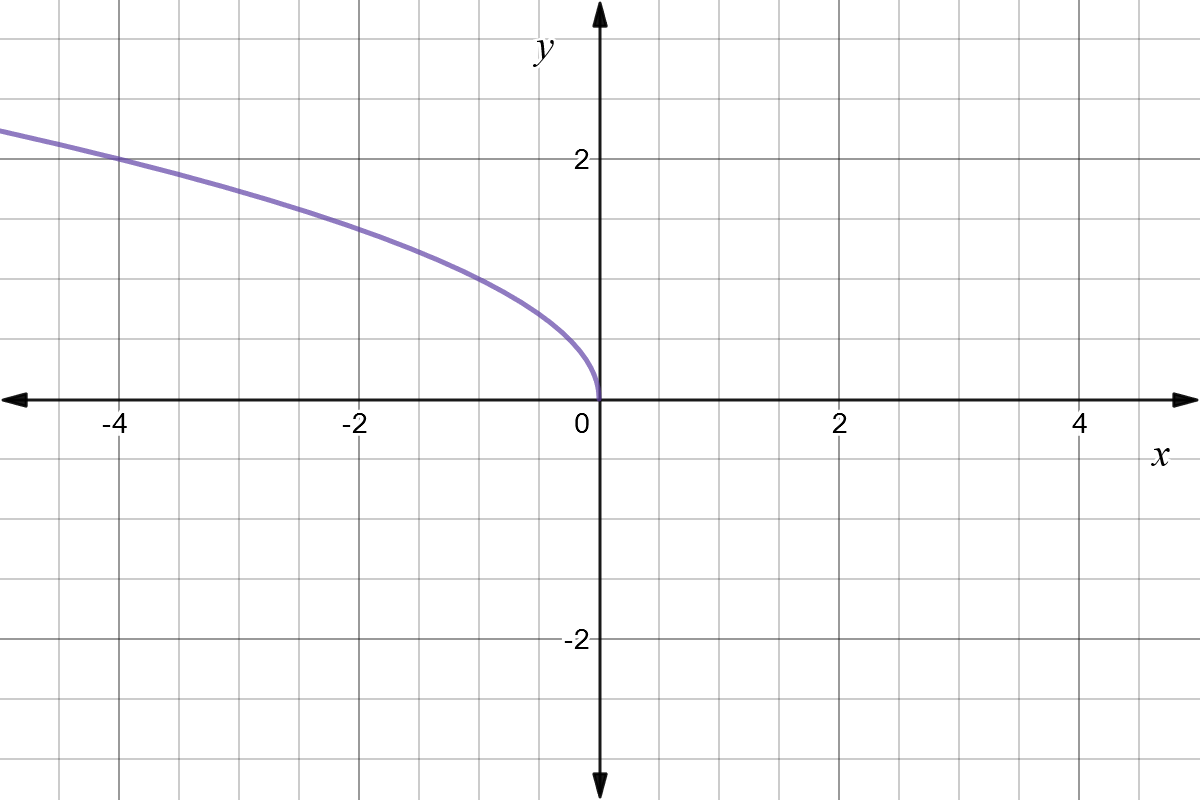


Reflect Function About Y Axis F X Expii



Translating And Scaling In Graphing Modified Functions What Is Translating And Scaling In Graphing Modified Functions Examples Solutions Cuemath
(A) 0 (B) 2 3 (D) 4 To answer this question we need to realise that we are looking for the value of y when x=0, We can see this from the question as we are told that y=f(x) So by drawing a line straight up from the origin to the curve we can see that when x=0, y=4Here is the Y = f(x) story, phase by phase Y = f(x) Process Outcome a Result of Process Inputs The mathematical term Y = f(x), which translates as simply "Y is a function of x," illustrates the idea that the important process outcomes (Ys) are a result of the drivers (x's) within processes The goal of DMAIC is to identify which few process and input variables mainly influence the processThe graph of the function is the set of all points latex\left(x,y\right)/latex in the plane that satisfies the equation latexy=f\left(x\right)/latex If the function is defined for only a few input values, then the graph of the function is only a few points, where the x coordinate of each point is an input value and the y coordinate
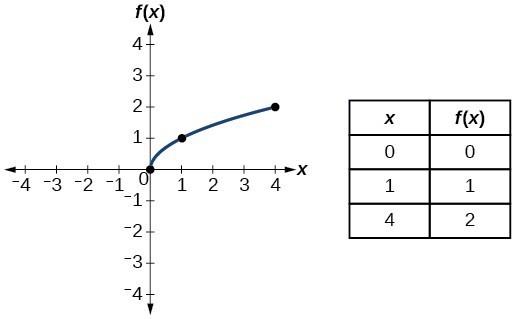


Identify Functions Using Graphs College Algebra
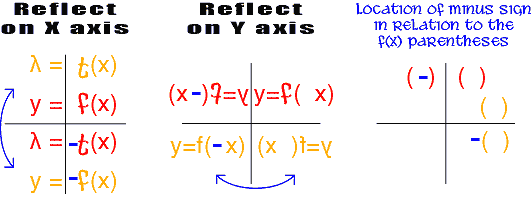


Squishy Function Graphs
The area between the graph of the function y = f(x) and the xaxis, starting at x = 0 is called the area function A(x) Example Find the area under the graph y = 2x between x = 2 and x = 4 The area between 2 and 4 can be described as area between x = 0 and x = 4 minus the area between x = 0 and x = 2 y = 2x Definite integrals/* then set temperature / Kelvin */ long double temperature = 3 * Kilo ();Y is the output measure, such as process cycle time or customer satisfaction f is the letter representing "function" (what the value (s) of X (s) does/do for Y (the output) X (s) is/are any process input (s) (variables) having assigned or inherent values (s) that is/are involved in producing the output For example, if you call your major department store to ask a question, the ability to


Math Scene Derivatives Lesson 2 Differentiating Polynomials



What Is Difference Between Math X F Y Math And Math Y F X Math Graph Quora
Sketch the graph of a function y = f(x) that satisfies the conditions Parent Functions Graphs & Examples In this lesson, you're going to learn about the difference between a family of• To graph y = f(x h), shift the graph of y = f(x) right hunits by adding hto the xcoordinates of the points on the graph of f In other words, Theorem13says that adding to or subtracting from the input to a functionI've since realised that 'y' can b


Injective Function Wikipedia


Graphing Reflections Y F X Or Y F X Youtube
Examples LiveMath notebook illustrating horizontal compressions and stretchings LiveMath notebook illustrating vertical compressions and stretchings Reflections Suppose that y = f (x) is a function;Depends on context In mathematics, Y is often used to represent the vertical axis of a graph In this context, f(x) is a function that takes a parameter x and returns a value A function is similar to a series of steps You give it a number and it gives you back something else Example of function f(x) = 5Next, pick points between these designated xvalues and substitute them into the equation for f' to determine the sign ( or ) for each of these intervals Beneath each designated xvalue, write the corresponding yvalue which is found by using the original equation y = f(x) These ordered pairs (x, y) will be a starting point for the graph


Use The Graph Of A Function To Graph Its Inverse College Algebra
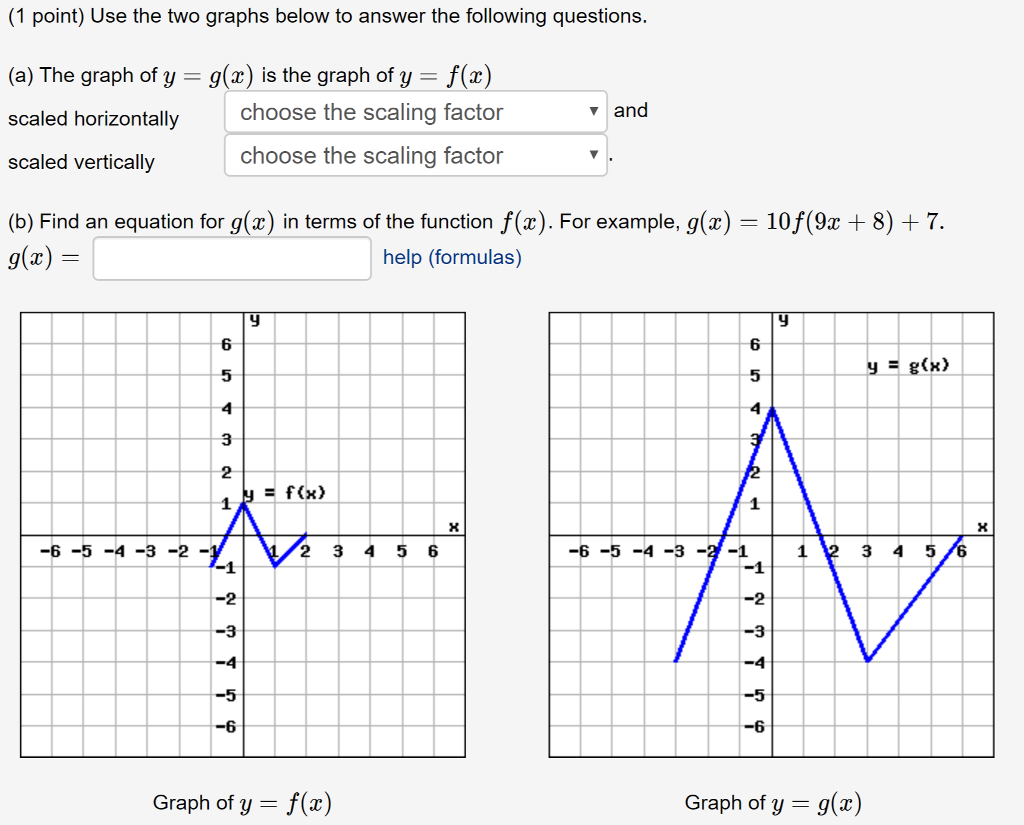


Solved 1 Point Use The Two Graphs Below To Answer The F Chegg Com
The graph of the function \(f(x)=x^3−4\) is the graph of \(y=x^3\) shifted down \(4\) units (Figure \(\PageIndex{9}\))Dec 09, 19 · y=f(x) will indicate that the graph has reflected about the origin If I have f(x)=(x) 3 , then the graph would be reflected about the yaxis Try to experiment on these transformations by using a graphing utility such as Desmos , Symbolab , GeoGebraC < 0 moves it down



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download



Common Functions Reference
The graph of f is the same as the graph of the equation y = f(x) Increasing/Decreasing Given a function f whose domain and range are subsets of the real numbers and is an interval contained within the domain, the function is called increasing on the interval I ifThe best way to start reasoning about limits is using graphs Learn how we analyze a limit graphically and see cases where a limit doesn't exist Google Classroom Facebook Twitter Email Estimating limit values from graphs Estimating limit values from graphs Unbounded limits


Integration Area And Curves


Igyh8zmz2lccm


Graphing Quadratic Functions
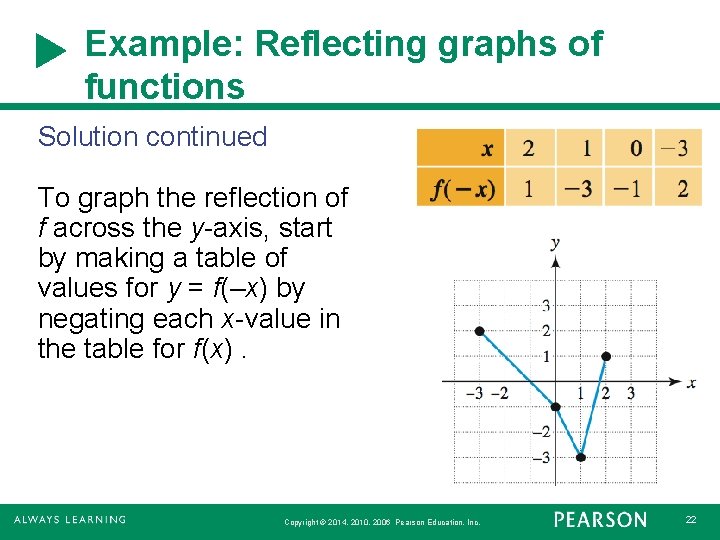


3 5 Transformations Of Graphs Graph Functions Using


Limit Of Function Examples Vertical Horizontal And Slant Or Oblique Asymptote Graphs Of Functions Examples
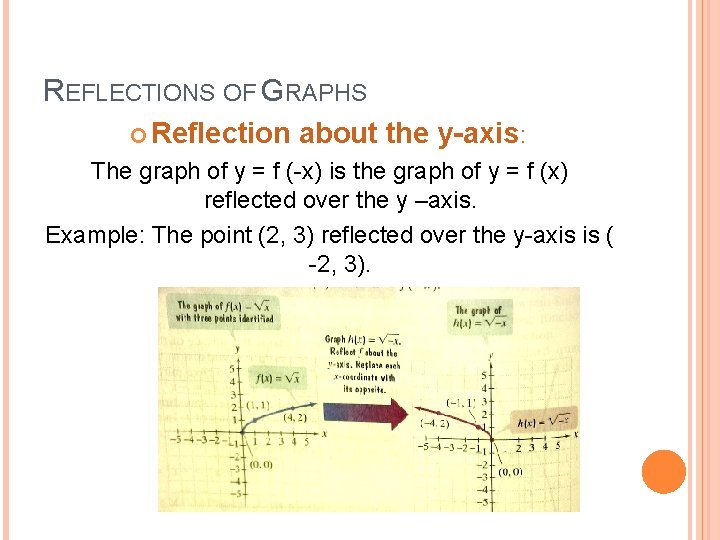


Functions And Graphs Aim 1 2 What Are
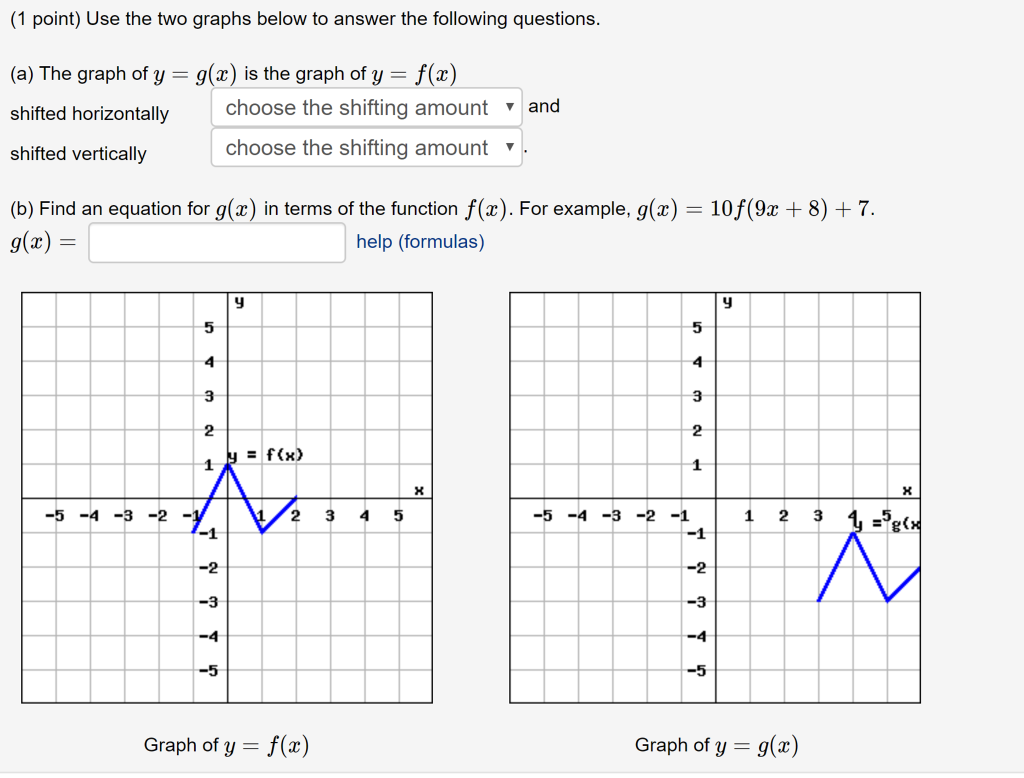


Solved 1 Point Use The Two Graphs Below To Answer The F Chegg Com


Sat Math Graph Example 2 Sat Math Forbest Academy


Graphs Of Functions


Function Definition Types Examples Facts Britannica
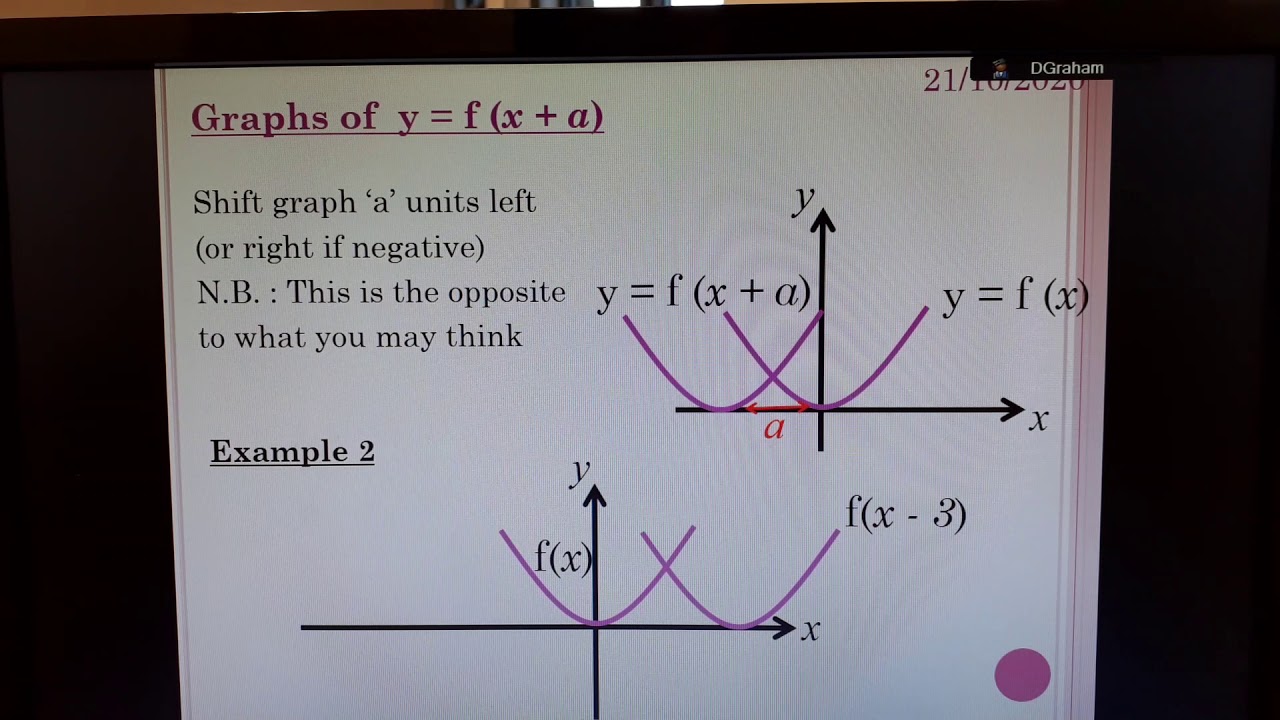


Higher Maths Graphs Of Functions Y F X A Youtube
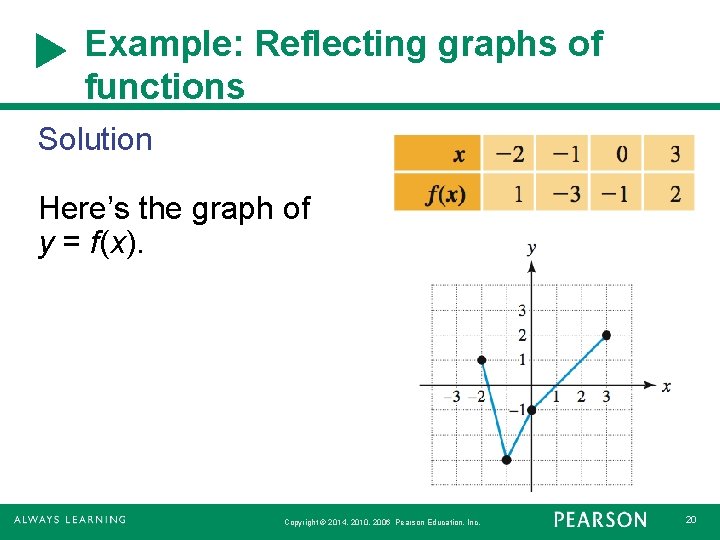


3 5 Transformations Of Graphs Graph Functions Using
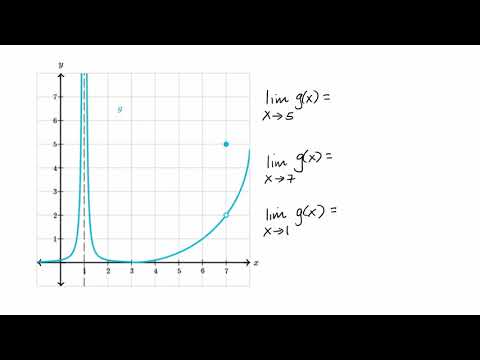


Estimating Limit Values From Graphs Video Khan Academy


Operations On Functions Stretches And Shrinks Sparknotes



Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation



Answered 0 2 2 2 2 2 2 E D F 2 Bartleby



Graph Of Y X And Y F X In Example 9 Download Scientific Diagram


Operations On Functions Translations Sparknotes



Transformation Of Graphs I Definition Examples Diagrams



Introduction To Limits In Calculus
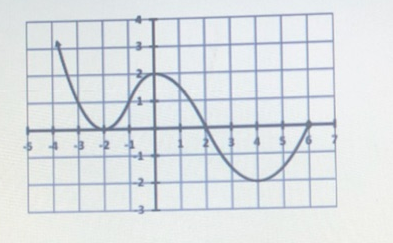


Y F X Is Given Graph Y F 3x 2 And Y F X 1 Socratic
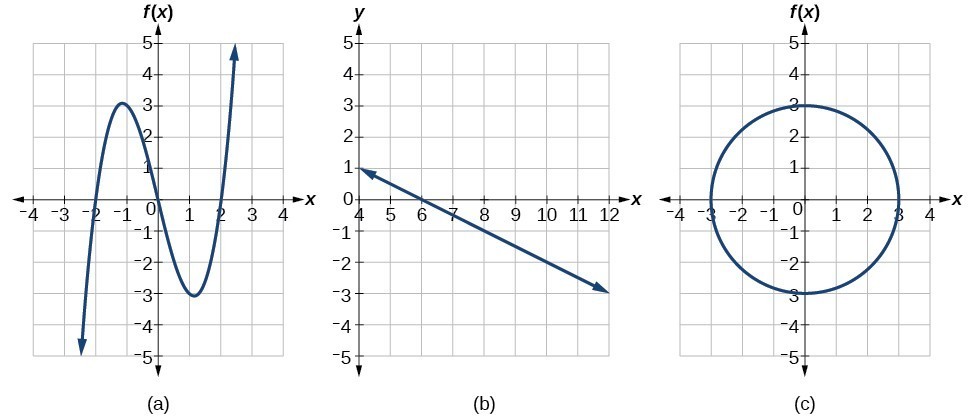


Identify Functions Using Graphs College Algebra



1 6 Graphs Of Functions
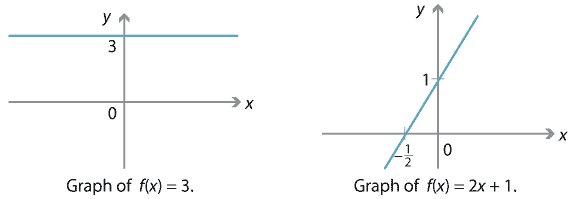


Content Polynomial Function Gallery
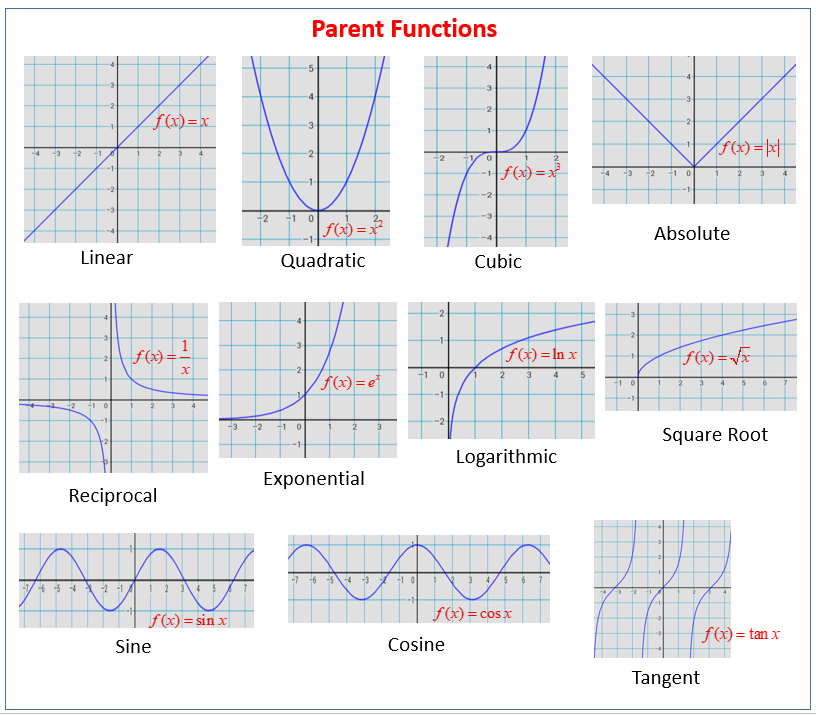


Parent Functions And Their Graphs Video Lessons Examples And Solutions



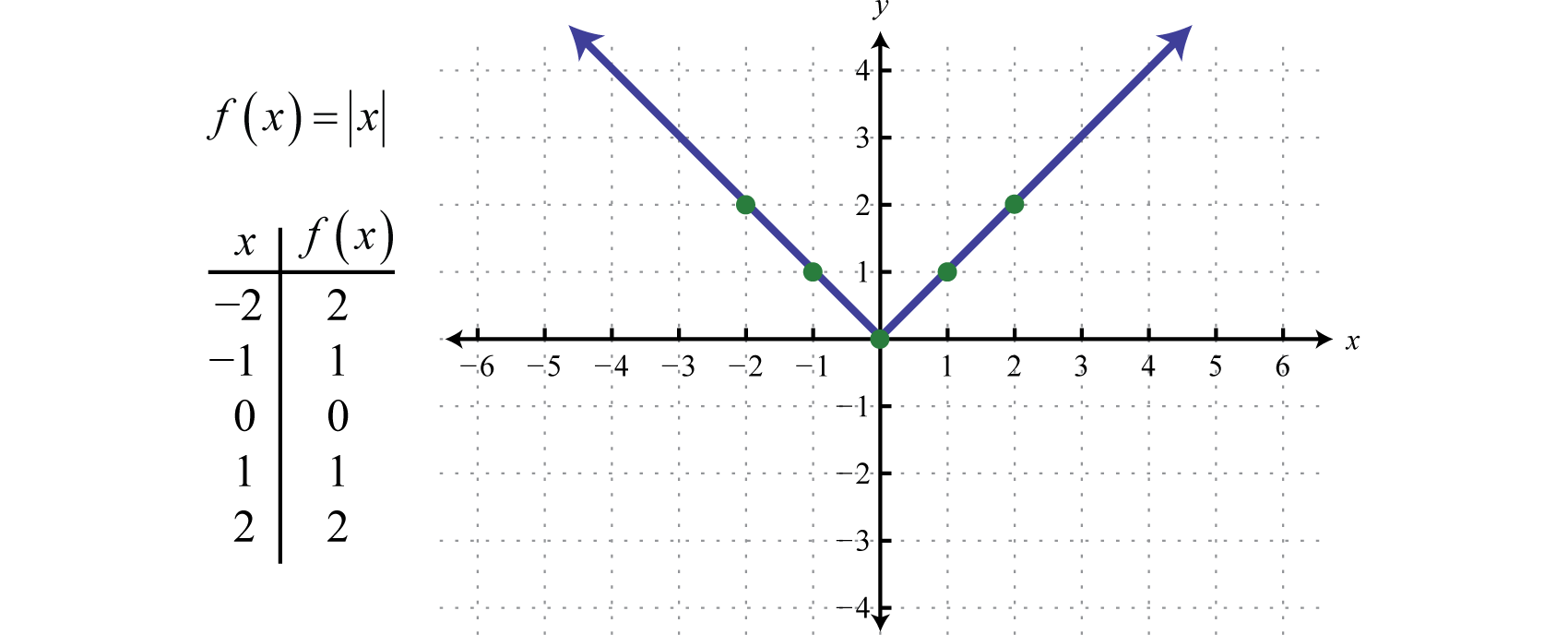
Absolute Value Graph And Function Review Article Khan Academy


One To One Function Explanation Examples



Reflect Function About Y Axis F X Expii
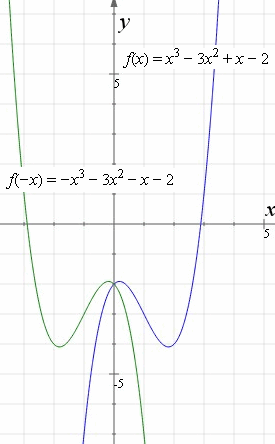


How To Reflect A Graph Through The X Axis Y Axis Or Origin


Graphs Of Y F X And Y F X Geogebra


Content Polynomials From Graphs


How To Reflect A Graph Through The X Axis Y Axis Or Origin


Day 2 Examples U2f13



Define The Function F R Gt R By Y F X X 2 X In R C


Discontinuous Functions


Graph Of A Function In 3d


F X F X 2 F X 2


Solution How Would F 1 Look On A Graph



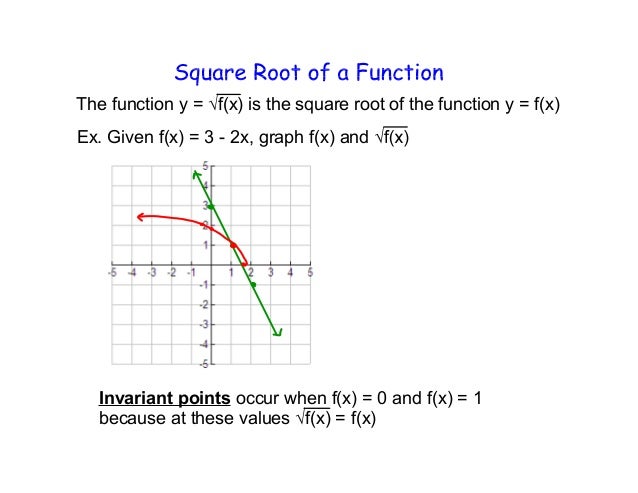
Graphing Square Root Functions


Graphing The Basic Functions


Operations On Functions Translations Sparknotes



Translations Of Graphs Iitutor


Reflecting Graphs
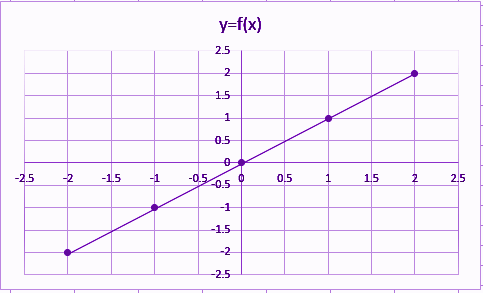


Identity Function Definition Graph Examples
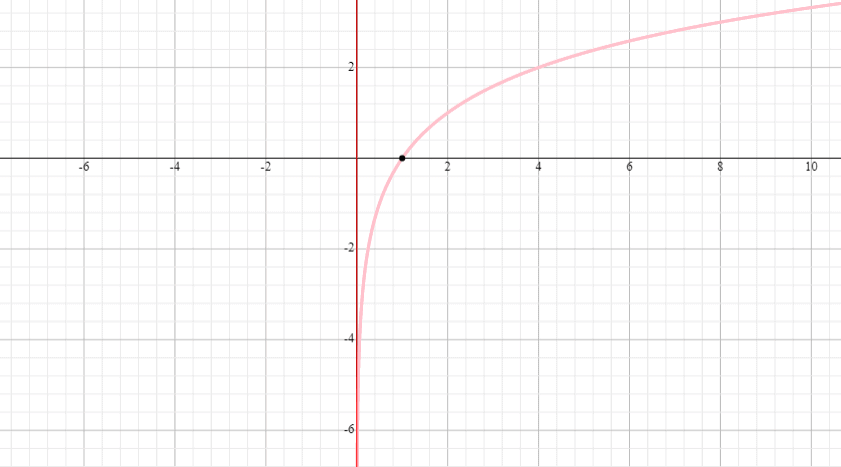


Graphs Of Logarithmic Function Explanation Examples



Answered Example 2 The Graphs Of Y F X And Y Bartleby
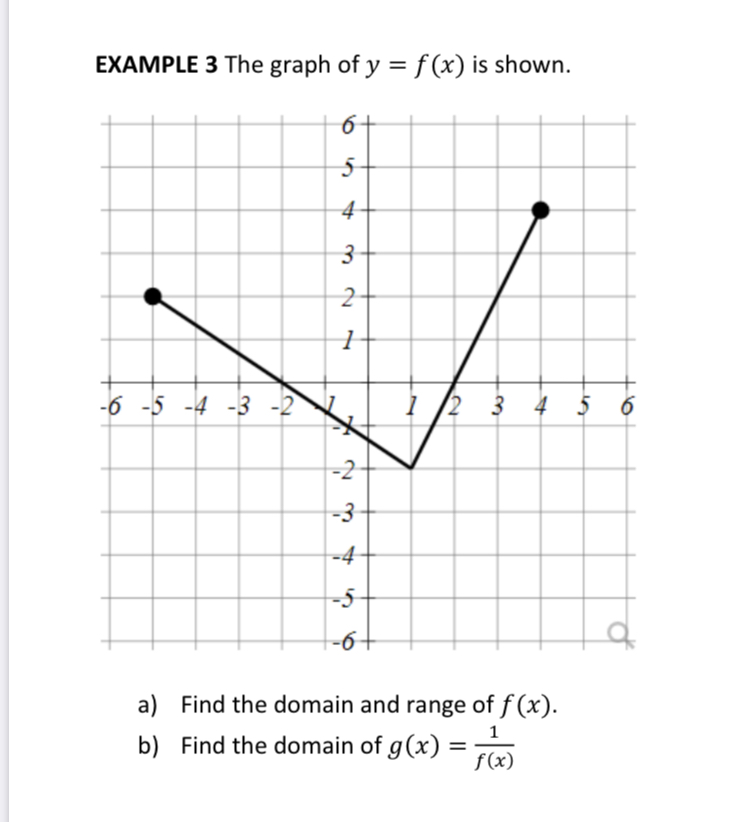


Answered Example 3 The Graph Of Y F X Is Bartleby
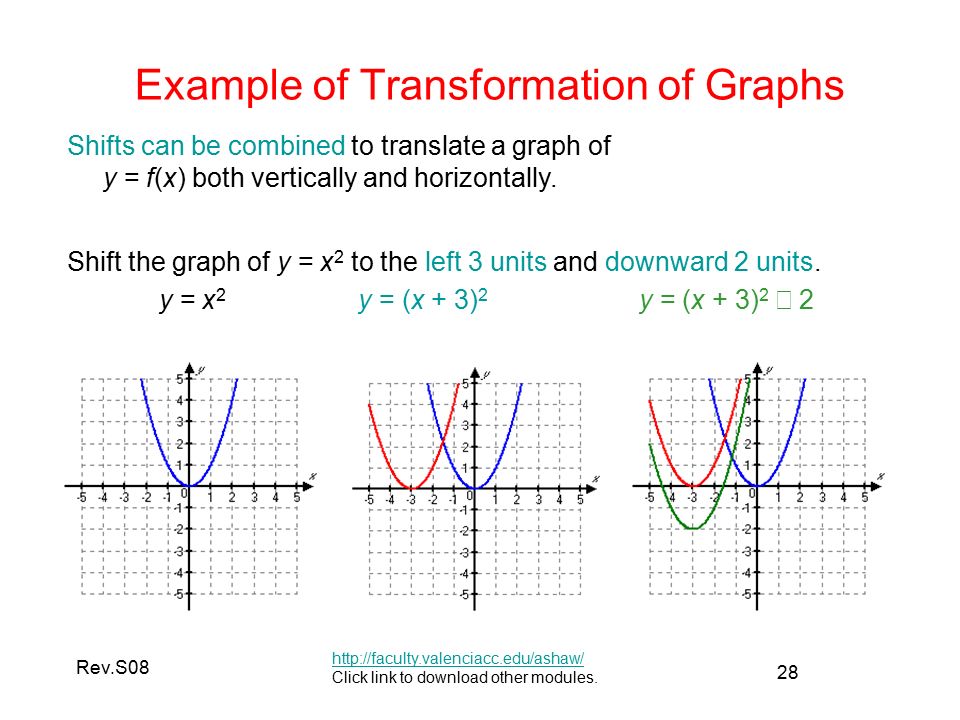


Transformation Of Graphs Ppt Video Online Download
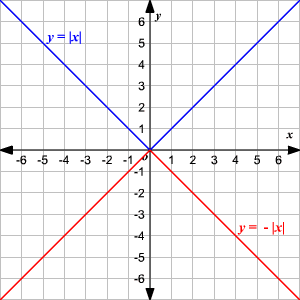


Absolute Value Functions
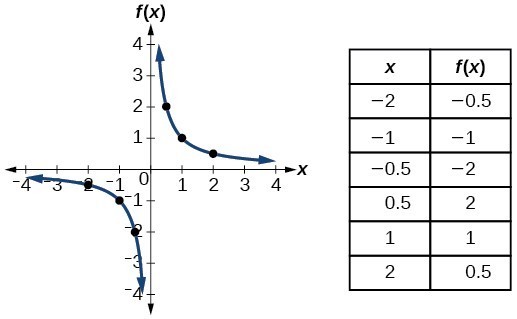


Identify Functions Using Graphs College Algebra
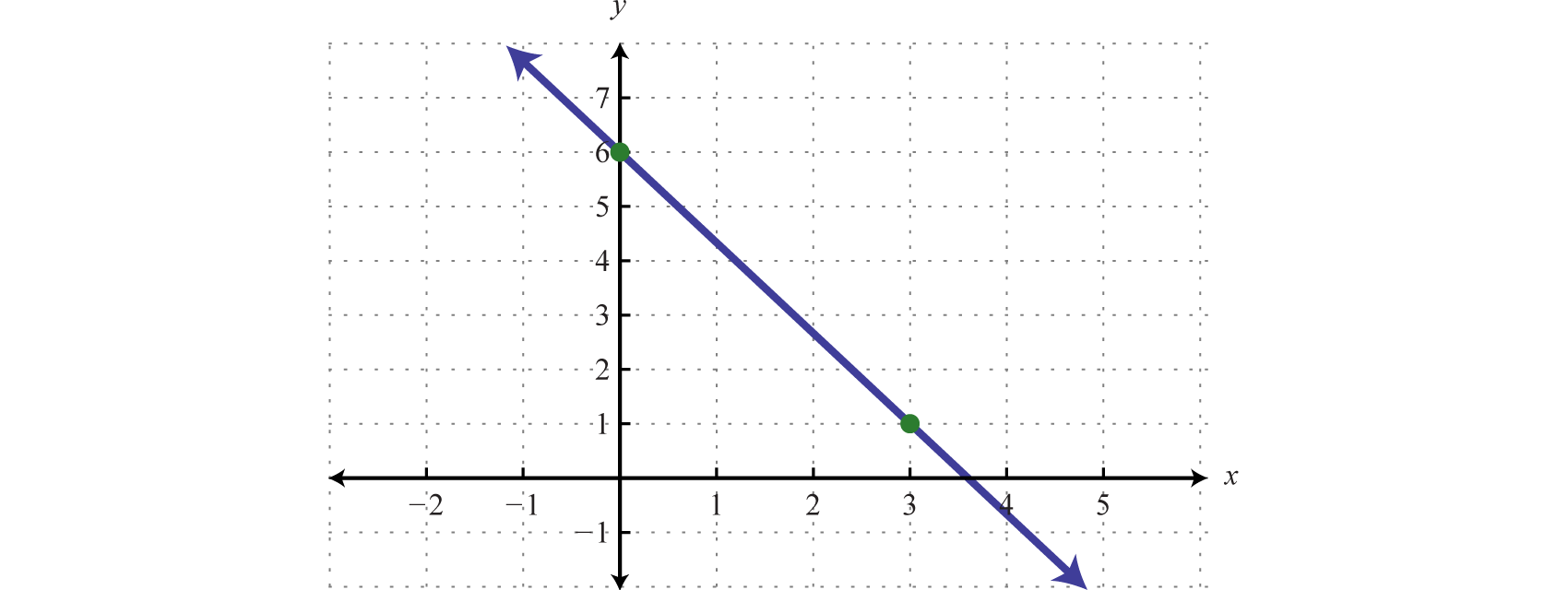


Linear Functions And Their Graphs



Shifting Of Graphs Transformation Example 1 Y F X Kup K Units Y F X Kdown K Units Vertical Shifting Below Is The Graph Of A Function Y Ppt Download
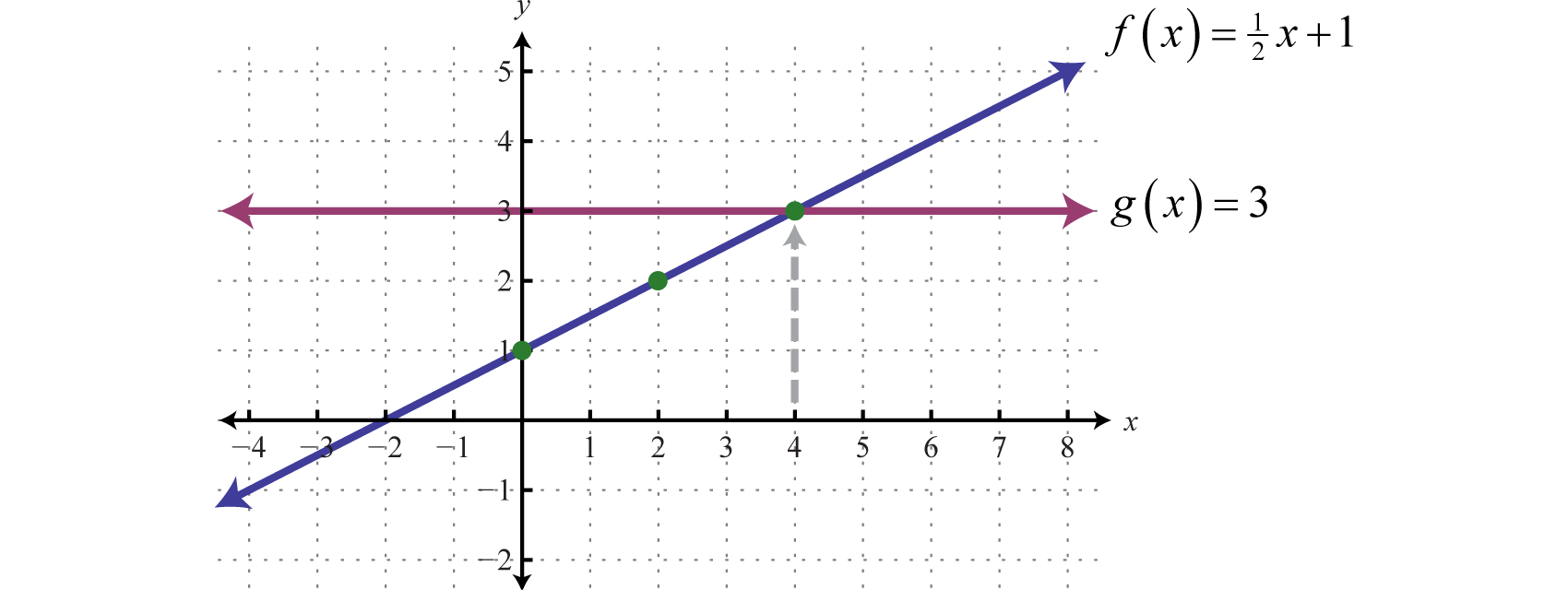


Linear Functions And Their Graphs
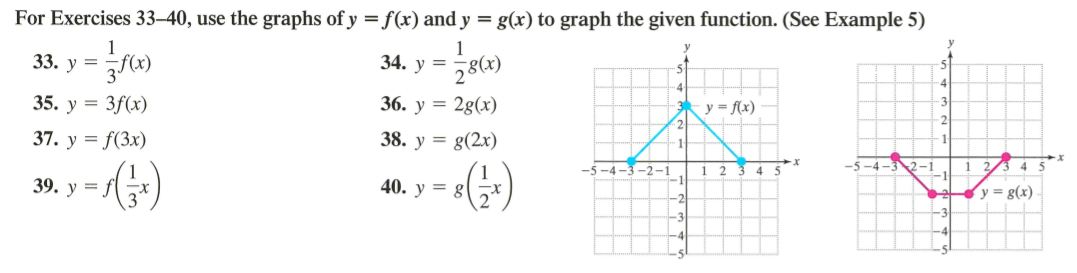


Solved For Exercises 33 40 Use The Graphs Of Y F X An Chegg Com


Use The Graph Of A Function To Graph Its Inverse College Algebra
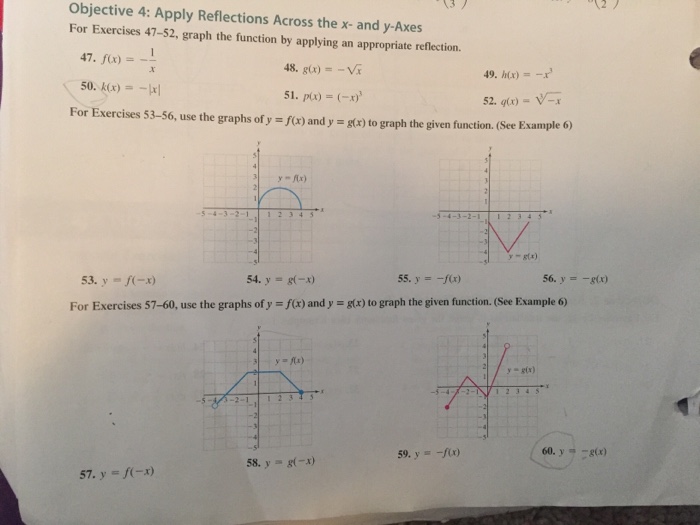


Solved Objective 4 Apply Reflections Across The X And Y Chegg Com
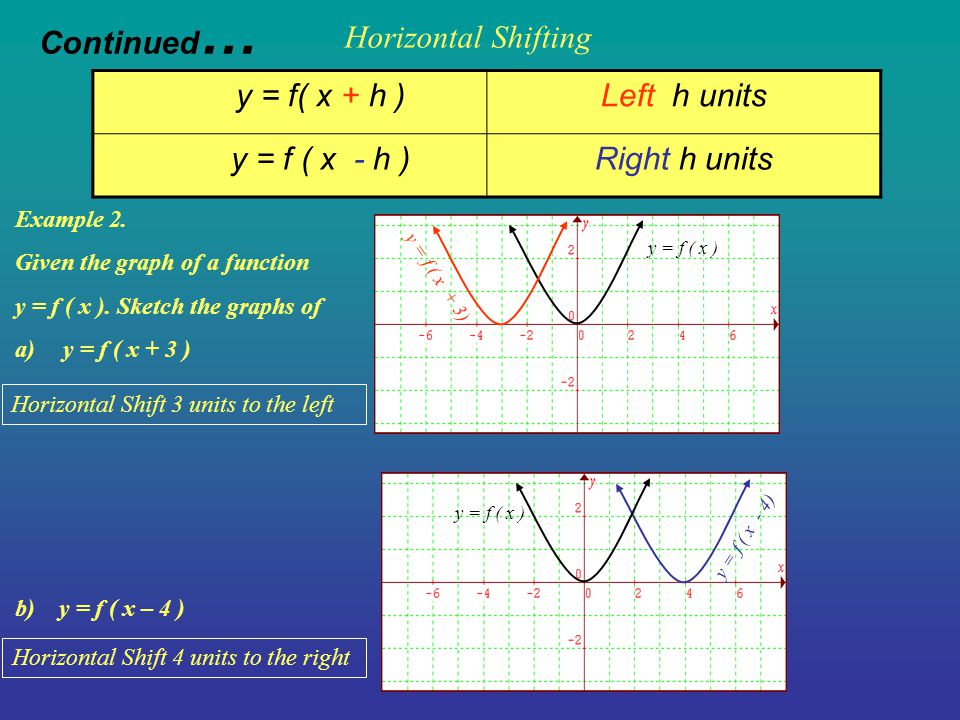


Shifting Of Graphs Transformation Example 1 Y F X Kup K Units Y F X Kdown K Units Vertical Shifting Below Is The Graph Of A Function Y Ppt Download
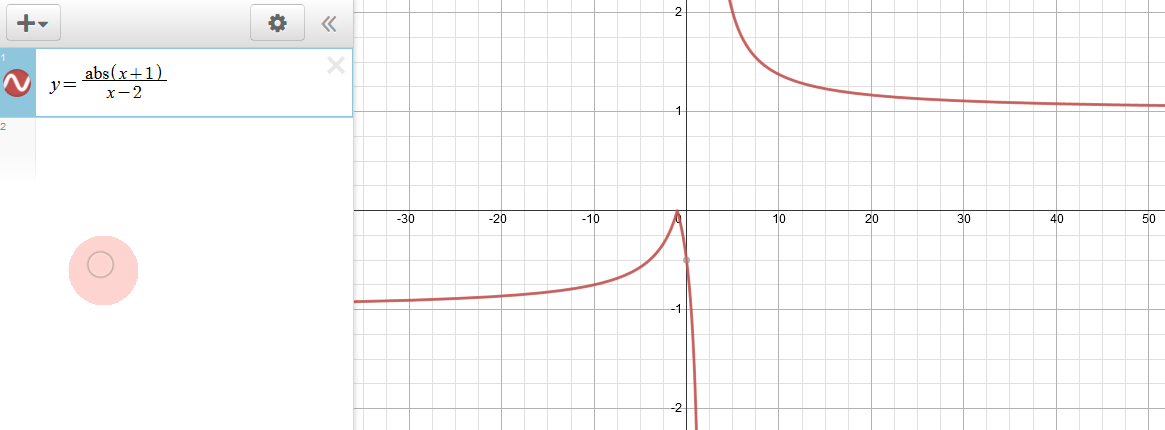


How Many Horizontal Asymptotes Can The Graph Of Y F X Have Socratic



Cc Constructing Accurate Graphs Of Antiderivatives
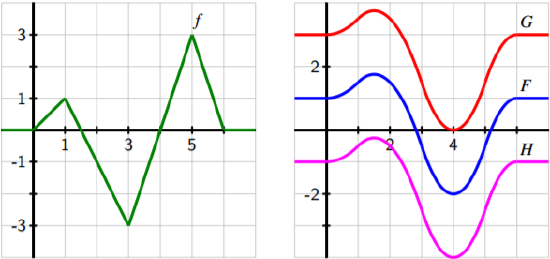


5 1 Construction Accurate Graphs Of Antiderivatives Mathematics Libretexts
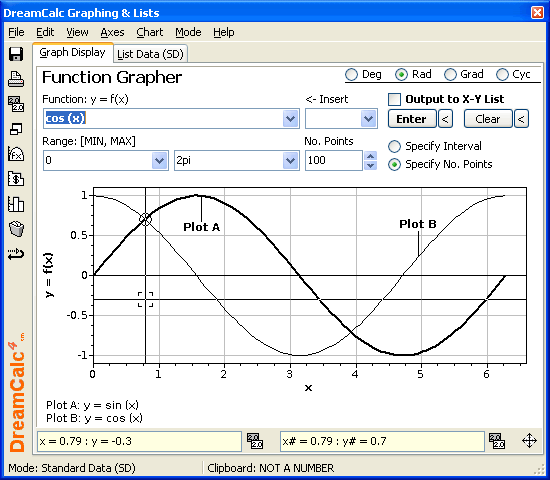


Graphing Calculator Graphing Examples



Graph Transformation Y F X A Of The Function F X Youtube



Graphs And Transformations Function Mathematics Cartesian Coordinate System



Graphing Functions With Excel
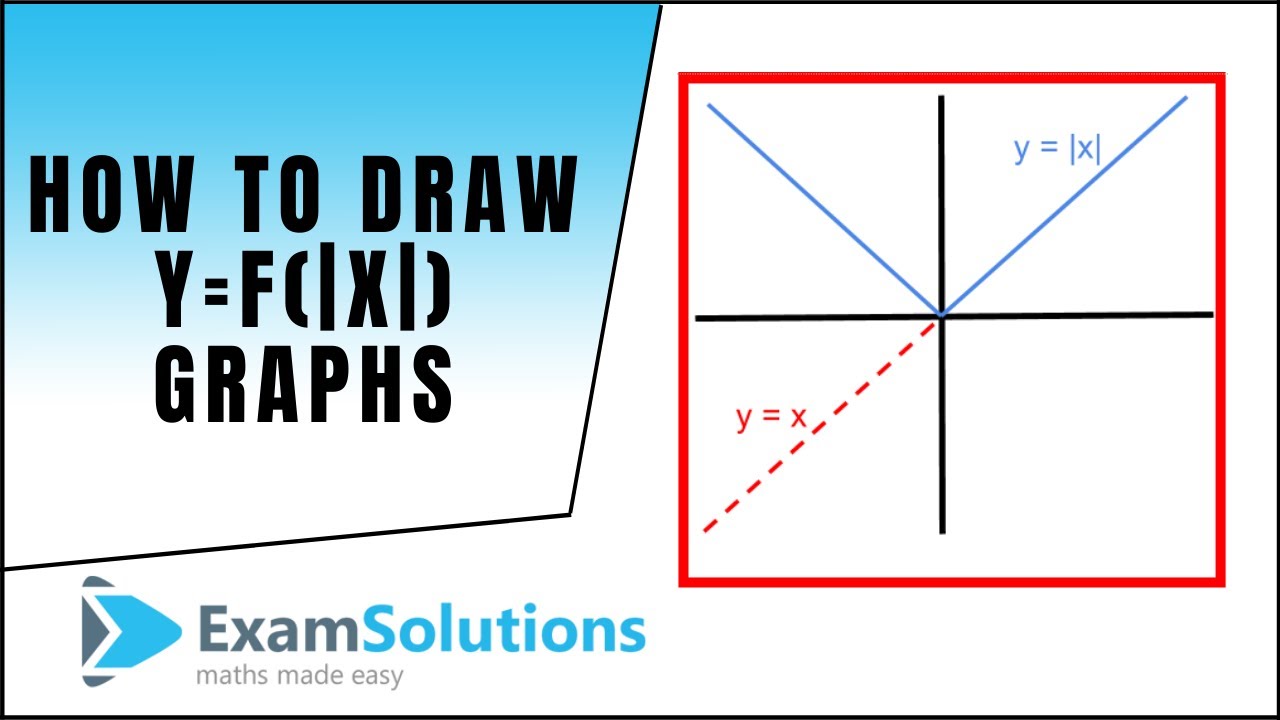


Graphing Y F X Examsolutions



Graph Of Y X And Y F X In Example 9 Download Scientific Diagram
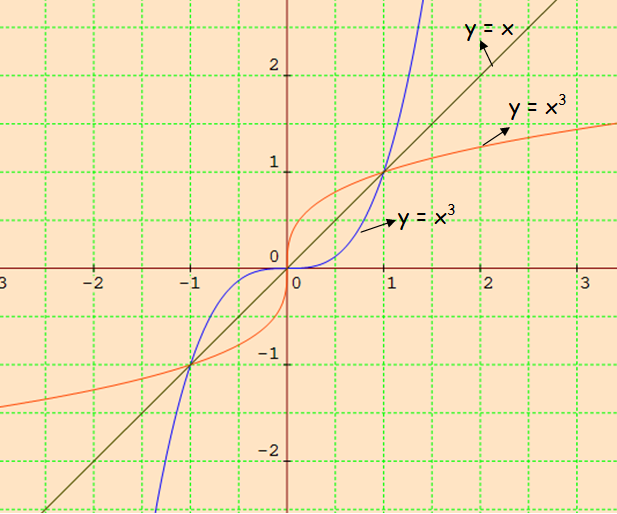


Graph The Function Using Transformations Examples



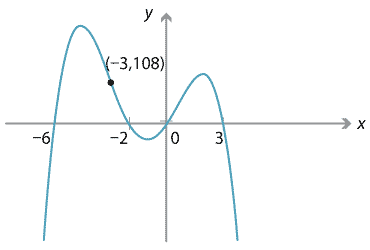
Use The Information Below To Sketch A Graph Of The Polynomial Function Y F X F X Is Positive On The Intervals Math Infty Math 3 2 0 And 2 3 F X Is Negative On The Intervals 3 2 0 2 And



Graphing Functions Free Sat Training
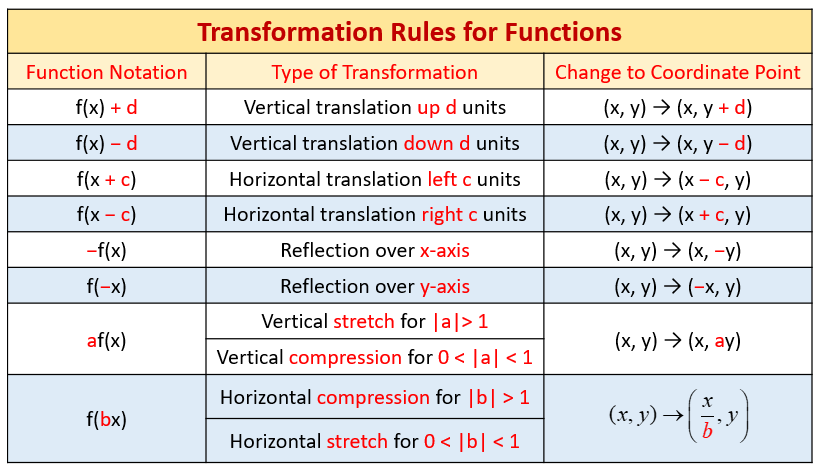


Parent Functions And Their Graphs Video Lessons Examples And Solutions



0 件のコメント:
コメントを投稿